cho tam giác ABC vuông tại A kẻ đường cao AH; lấy K;I lần lượt là trung điểm của HC;AH chứng minh
a.IK vuông góc với AB
b.BI vuông góc với AK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 9 2017
Ta có: H B H C = 1 4 ⇒ HC = 4HB
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
A H 2 = B H . C H ⇔ 4 2 = 4 B H 2 ⇔ B H = 2 ( c m ) ⇒ C H = 8 ( c m )
Ta có: BC = BH + HC = 2 + 8 = 10 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
⇒ A B 2 = B H . B C ⇔ A B 2 = 2 . 10 ⇔ A B = 20 = 2 5 ( c m )
Áp dụng định lý Pitago cho ABH vuông tại A có: A B 2 + A C 2 = B C 2
⇔ 20 + A C 2 = 100 ⇔ A C 2 = 80 ⇒ A C = 80 = 4 5 ( c m )
Vậy chu vi tam giác ABC là: 4 5 + 2 5 + 10 = 6 5 + 10 c m
Đáp án cần chọn là: D
MT
22 tháng 7 2018
BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= =
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= =4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:
·
KT
22 tháng 7 2018
Bài 1:
A B C H E
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)
23 tháng 12 2023
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
b: Xét tứ giác AHKC có
I là trung điểm chung của AK và HC
=>AHKC là hình bình hành
=>AC//KH
c: Ta có: AC//HK
AC//HM
HK,HM có điểm chung là H
Do đó: K,H,M thẳng hàng
Ta có: AMHN là hình chữ nhật
=>\(\widehat{NAH}=\widehat{NMH}\)
mà \(\widehat{NAH}=\widehat{CKH}\)(AHKC là hình bình hành)
nên \(\widehat{NMH}=\widehat{CKH}\)
Xét tứ giác MNCK có CN//MK
nên MNCK là hình thang
Hình thang MNCK có \(\widehat{CKM}=\widehat{NMK}\)
nên MNCK là hình thang cân
d: Ta có: AMHN là hình chữ nhật
=>AH cắt MN tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và MN
Xét ΔCAH có
CO,AI là các đường trung tuyến
CO cắt AI tại D
Do đó: D là trọng tâm của ΔCAH
=>\(AD=\dfrac{2}{3}AI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AK=\dfrac{1}{3}AK\)
=>AK=3AD
2 tháng 3 2022
Xét \(\Delta ABC\) vuông tại A, đường cao AH:
\(AH^2=CH.BH\) (Hệ thức lượng).
\(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}.\)
Xét \(\Delta ABH\) và \(\Delta CAH:\)
\(\widehat{AHB}=\widehat{CHA}=\left(90^o\right).\\ \dfrac{AH}{CH}=\dfrac{BH}{AH}\left(cmt\right).\\ \Rightarrow\Delta ABH\sim\Delta CAH\left(c-g-c\right).\)
22 tháng 6 2023
Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
góc B chung
=>ΔAHB đồng dạng với ΔCAB
=>BA/BC=BH/BA
=>BA^2=BH*BC
5 tháng 11 2021
a, \(AB=\sqrt{BC^2-AC^2}=24\left(cm\right)\left(pytago\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx53^0\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=19,2\left(cm\right)\\CH=\dfrac{AC^2}{BC}=10,8\left(cm\right)\\AH=\sqrt{BH\cdot CH}=14,4\left(cm\right)\end{matrix}\right.\)
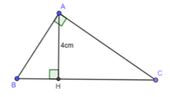
a/ Ta có
\(IA=IH;KC=KH\left(gt\right)\) => IK là đường trung bình của tg AHC => IK//AC
Mà \(AC\perp AB\)
\(\Rightarrow IK\perp AB\)
b/ Xét tg ABK có
\(AH\perp BK;IK\perp AB\) => I là trực tâm của tg ABK => \(BI\perp AK\) (trong tg 3 đường cao đồng quy)