Giải hệ PT:
4x-2y=3
6x-3y=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PH
1
H9
HT.Phong (9A5)
CTVHS
3 tháng 7 2023
a) \(\left\{{}\begin{matrix}2x+3y=5\\4x-5y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+6y=10\\4x-5y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+3y=5\\11y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+3\cdot\dfrac{9}{11}=5\\y=\dfrac{9}{11}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{27}{11}=5\\y=\dfrac{9}{11}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=\dfrac{28}{11}\\y=\dfrac{9}{11}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{14}{11}\\y=\dfrac{9}{11}\end{matrix}\right.\)
Vậy: \(x=\dfrac{14}{11};y=\dfrac{9}{11}\)
20 tháng 9 2021
\(a,\left\{{}\begin{matrix}3x-y=5\\4x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-y=5\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\\ b,\left\{{}\begin{matrix}5x+2y=9\\x+5y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+2y=9\\5x+25y=55\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+2y=9\\23y=46\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
\(c,\left\{{}\begin{matrix}3x+y=10\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+3y=30\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=39\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\\ d,\left\{{}\begin{matrix}4x+3y=22\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=2\end{matrix}\right.\)
\(e,\left\{{}\begin{matrix}4x-3y=5\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=18\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
HP
20 tháng 9 2021
a. \(\left\{{}\begin{matrix}3x-y=5\\4x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-2y=10\\4x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x=20\\6x-2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
b. \(\left\{{}\begin{matrix}5x+2y=9\\x+5y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+2y=9\\5x+25y=55\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}23y=46\\5x+2y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}3x+y=10\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+3y=30\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=39\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
d. \(\left\{{}\begin{matrix}4x+3y=22\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\4x+3y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=2\end{matrix}\right.\)
e. \(\left\{{}\begin{matrix}4x-3y=5\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=18\\4x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
OP
0
T
6
11 tháng 5 2020
Ta có \(\hept{\begin{cases}xy^2+2x-4y=-1\\x^2y^3+2xy^2-4x+3y=2\end{cases}\left(I\right)}\)
Ta có \(\left(I\right)\Leftrightarrow\hept{\begin{cases}x^2+\left(y+1\right)^2-x\left(y+1\right)=1\\2x^2=x+y+1\end{cases}}\left(II\right)\)
Đặt t=y+1 ta có hệ
\(\left(II\right)\Leftrightarrow\hept{\begin{cases}x^2+t^2-xt=1\\2x^3=\left(x+t\right)\left(x^2+t^2-xt\right)\end{cases}\Leftrightarrow\hept{\begin{cases}x^2+t^2-xt=1\\x=t\end{cases}\Leftrightarrow}\hept{\begin{cases}x=t=1\\x=t=-1\end{cases}}}\)
Với x=t=1 => y=0
Với x=t=-1 => y=-2
Vậy nghiệm hệ là (1;0);(-1;-2)
KN
11 tháng 5 2020
\(\hept{\begin{cases}xy^2+2x-4y=-1\\x^2y^3+2xy^2-4x+3y=2\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}xy^2+\left(2x+1\right)=4y\\\left(x^2y^2+2xy+1\right)y-2\left(2x+1\right)=-2y\end{cases}}\)(*)
- Xét y = 0 thay vào hệ (*), ta được hệ phương trình: \(\hept{\begin{cases}2x+1=0\\-2\left(2x+1\right)=0\end{cases}}\Leftrightarrow x=\frac{-1}{2}\)
Suy ra \(\left(\frac{-1}{2};0\right)\)là một nghiệm của hệ.
- Xét \(y\ne0\), hệ (*) tương đương với: \(\hept{\begin{cases}xy+\frac{2x+1}{y}=4\\x^2y^2+2xy+1-2\left(\frac{2x+1}{y}\right)=-2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(xy+1\right)+\frac{2x+1}{y}=5\\\left(xy+1\right)^2-2\left(\frac{2x+1}{y}\right)=-2\end{cases}}\)(**)
Đặt \(a=xy+1;b=\frac{2x+1}{y}\), khi đó hệ (**) trở thành: \(\hept{\begin{cases}a+b=5\\a^2-2b=-2\end{cases}}\)(***)
Giải hệ (***) tìm được \(\hept{\begin{cases}a=2\\b=3\end{cases}}\)hoặc \(\hept{\begin{cases}a=-4\\b=9\end{cases}}\)
* Với \(\hept{\begin{cases}a=2\\b=3\end{cases}}\)thì \(\hept{\begin{cases}xy+1=2\\\frac{2x+1}{y}=3\end{cases}}\Leftrightarrow\hept{\begin{cases}x\left(\frac{2x+1}{3}\right)=1\\y=\frac{2x+1}{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}\)hoặc \(\hept{\begin{cases}x=-\frac{3}{2}\\y=-\frac{2}{3}\end{cases}}\)
* Với \(\hept{\begin{cases}a=-4\\b=9\end{cases}}\)thì \(\hept{\begin{cases}xy+1=-4\\\frac{2x+1}{y}=9\end{cases}}\Leftrightarrow\hept{\begin{cases}x\left(\frac{2x+1}{9}\right)=-5\\y=\frac{2x+1}{9}\end{cases}}\)(vô nghiệm)
Vậy hệ phương trình có 3 nghiệm \(\left(x;y\right)\in\left\{\left(-\frac{1}{2};0\right);\left(1;1\right);\left(-\frac{3}{2};-\frac{2}{3}\right)\right\}\)
22 tháng 2 2022
a, Ta có : \(\dfrac{4}{6}=-\dfrac{2}{-3}\ne\dfrac{5}{5}=1\)
vậy hpt vô nghiệm
b, Ta có \(\dfrac{2}{4}=\dfrac{3}{6}=\dfrac{5}{10}\)-> hệ pt có vô số nghiệm
15 tháng 2 2023
Đặt 1/(x+2y)=a; y=b
=>a+b=-2 và 2a-3b=1
=>a=-1; b=-1
=>y=-1; x+2y=-1
=>y=-1; x=-1-2y=-1-2*(-1)=-1+2=1
CM
19 tháng 2 2019
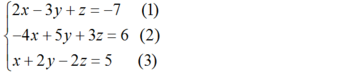
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần các ẩn.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (3) với 4 rồi cộng với phương trình (2) ta được:
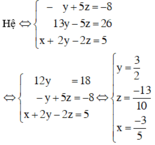
Vậy hệ phương trình có nghiệm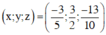 
\(\int^{4x-2y=3}_{6x-3y=5}\Leftrightarrow\int^{12x-6y=9}_{12x-6y=10}\Leftrightarrow\int^{0=1}\Rightarrow hpt_{ }\) VÔ NGHIỆM
pt vô nghiệm , cái này dễ mà, chỉ việc bấm máy