Cho tam giác ABC nhọn(AB>BC).Gọi M,N,P lần lượt là trung điểm AB,AC,BC.Trên tia đối tia NM lấy D sao cho ND=NM.Chứng minh a) Tứ giác BMNP là hình bình hành b)BN//DP c)PN đi qua trung điểm AD d)Gọi MC cắt PD ở E. Chứng minh DE=2PE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có: MN//BC
D\(\in\)NM
Do đó; MD//CB
ta có: \(MN=\dfrac{CB}{2}\)
\(MN=\dfrac{MD}{2}\)
Do đó:CB=MD
Xét tứ giác BMDC có
BC//MD
BC=MD
Do đó: BMDC là hình bình hành
b: Xét tứ giác AMCD có
N là trung điểm chung của AC và MD
nên AMCD là hình bình hành

a: Xét tứ giác BMCD có
N là trung điểm chung của BC và MD
=>BMCD là hình bình hành
b: Ta có: BMCD là hình bình hành
=>BM//CD và BM=CD
Ta có: BM//CD
M\(\in\)AB
Do đó: AM//CD
ta có: BM=CD
AM=MB
Do đó: AM=CD
Xét tứ giác AMDC có
AM//DC
AM=DC
Do đó: AMDC là hình bình hành
Hình bình hành AMDC có \(\widehat{MAC}=90^0\)
nên AMDC là hình chữ nhật
c: Ta có: AMDC là hình chữ nhật
=>\(\widehat{DMA}=90^0\)
=>DM\(\perp\)AB tại M
Xét ΔDBA có
DM là đường cao
DM là đường trung tuyến
Do đó: ΔDBA cân tại D

Bạn tham khảo ở đây:
Câu hỏi của Công chúa thủy tề - Toán lớp 7 - Học toán với OnlineMath

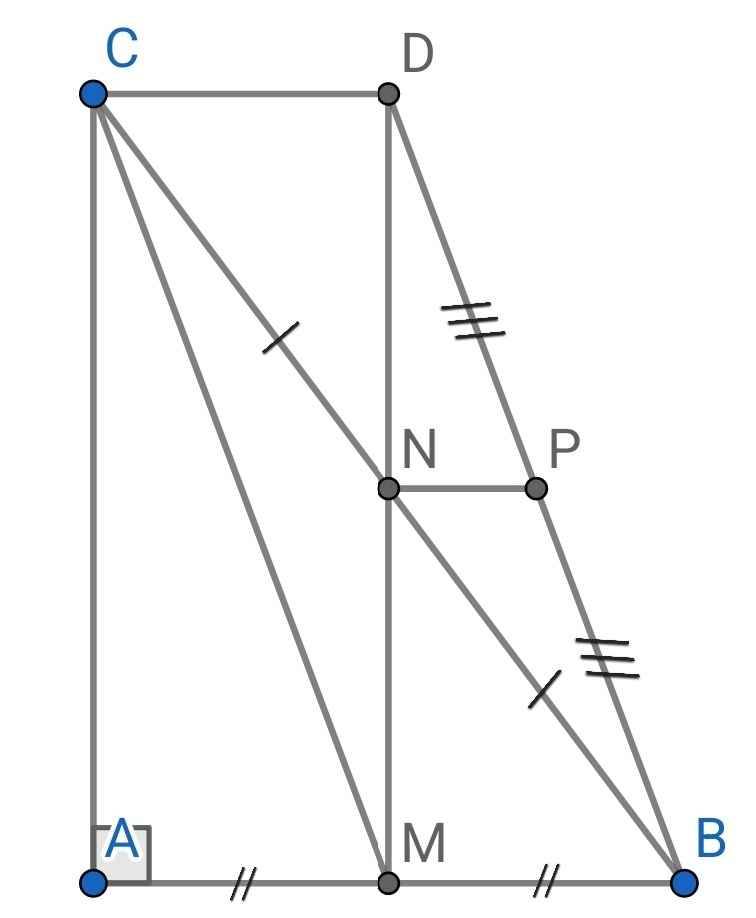 a) Do NM = ND (gt)
a) Do NM = ND (gt)
N ∈ MD
⇒ N là trung điểm của MD
Tứ giác BMCD có:
N là trung điểm của BC (gt)
N là trung điểm của MD (cmt)
⇒ BMCD là hình bình hành
b) Do M là trung điểm của AB (gt)
N là trung điểm của BC (gt)
⇒ MN // AC
⇒ MD // AC
Mà AC ⊥ AM (AB ⊥ AC)
⇒ MD ⊥ AM
⇒ ∠AMD = 90⁰
Do BMCD là hình bình hành (cmt)
⇒ CD // BM
⇒ CD // AM
Mà AM ⊥ AC (cmt)
⇒ CD ⊥ AC
⇒ ∠ACD = 90⁰
Tứ giác AMDC có:
∠CAM = ∠ACD = ∠AMD = 90⁰
⇒ AMDC là hình chữ nhật
c) ∆DMB có:
N là trung điểm của DM (cmt)
P là trung điểm của BD (gt)
⇒ NP // BM
⇒ NP // AB

a) Tứ giác AMCD có 2 đường chéo cắt nhau tại trung điểm mỗi đường => AMCD là hình bình hành
=> AD // MC.
b) Theo câu a) tứ giác AMCD là hình bình hành => CD // AM và CD = AM.
Mà AM = MB và đường thẳng AM cũng là đường thẳng MB
=> CD song song và bằng MB
=> MBCD là hình bình hành vì có 2 cạnh đối song song và bằng nhau
=> BC = MD
Mà MD = 2 MN => BC = 2 MN
a) Có thể chứng minh cách khác:
Tam giác NAD băng tam giác NCM theo trường hợp C-G-C
=> \(\widehat{NAD}=\widehat{NCM}\)
=> AD // MC vì có 2 góc so le bằng nhau.
b) Vì tam giác NAD bằng tam giác NCM nên AD = MC, lại có AD // MC nên AMCD là hình bình hành
=> CD song song và bằng AM, mà AM = MB và đường thẳng AM và MB trùng nhau nên CD song song và bằng MB
=> MBCD là hình bình hành => BC = MD mà MD = 2 MN => BC = 2 MN.

Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra:MN//BC
hay BMNC là hình thang

Bạn Minh Anh bạn đã tìm được đáp án ch vậy , cho tôi xin đáp án với vì câu hỏi của tôi y hệt bạn mà hỏi kh ai trl