ai làm giúp mik bài 5 trang 55 sgk lớp 7 với tặng 1 like cho người làm đúng
lớp 7 nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
4
4 tháng 3 2021
1)
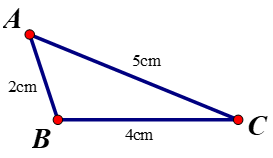
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
2)heo định lý tổng ba góc trong tam giác ABC, ta có:
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Kiến thức áp dụng
+ Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
+ Định lý tổng ba góc trong tam giác: Trong một tam giác, tổng ba góc bằng 180º.
3 a) Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
b) Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có
4) Trong một tam giác ta luôn có:
+ Góc đối diện với cạnh lớn hơn là góc lớn hơn
⇒ góc đối diện với cạnh nhỏ nhất là góc nhỏ nhất.
+ Góc nhỏ nhất luôn là góc nhọn.
(Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn
⇒ Góc nhỏ nhất ≥ 90º ⇒ cả ba góc ≥ 90º ⇒ tổng ba góc trong tam giác ≥ 90º.3 = 270º.
5) + Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).
+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :
nên góc ABD cũng là góc tù.
Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD
(2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy Hạnh đi xa nhất, Trang đi gần nhất.
6)Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.
7)
a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.
⇒ tia B’B nằm giữa hai tia BA và BC.
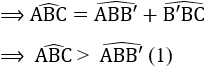
b) ∆ABB’ có AB = AB’ nên ∆ABB’ cân tại A.
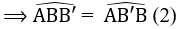
c) Vì góc AB'B là góc ngoài tại B’ của ∆BB’C
TH
0
A
5
TL
11 tháng 2 2019
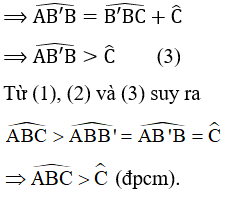
54. Đoạn lên dốc từ C đến A dài 8.5cm, đô dài CB bằng 7,5cm.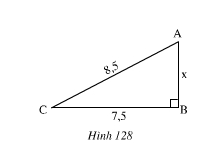
Tính chiều cao AB.
Theo địnhlípytago, ta có:
AB2 + BC2 = AC2
nên AB2 = AC2 – BC2
= 8,52 – 7,52
= 72,5-56,5=16
Vậy AB= 4
Bài 55 trang 131.Tính chiều cao của bức tường(h.129) biết rằng chiều cao của thang là 4m và chân thang cách tường 1m.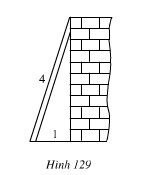
Theo đL pytago, ta có:
AC2+ BC2 = AB2
nên AC2 = AB2+BC2
Suy ra LAD = √15 ≈ 3.87
Luyện tập 1:
Bài 56 Toán 7 tập 1. Tam giác nào là Δvuông trong các Δcó độ dài ba cạnh như sau:
a) 9cm,15cm,12cm.
b) 5dm,13dm,12cm.
c)7m,7m,10m.
Đáp án: a) Ta có 92 = 81,152 = 225, 122 =144.
mà 225=81+144
hay 152=92+122.
Nên Δ có độ dài ba cạnh 9cm,15cm,12cm là Δ vuông.
b) Ta có 52=25,132=169,122=144.
Mà 169=25+144 nên Δ có độ dài ba cạnh 5dm, 13dm,12dm là Δvuông
c) Ta có 72=49, 102=100
vậy 72+ 72 ≠102
72+102 ≠72
Nên Δ có độ dài 3 canh là 7dm,7dm,10dm không phải là Δvuông.
11 tháng 2 2019
Bài 54:
Theo định lí Pytago, ta có:
AB2+BC2=AC2
nên AB2=AC2–BC2
\(8.5^2-7.5^2\)
=72,5−56,5=16=
Vậy Ab =4 cm
Bài 55:
Theo đL pytago, ta có:
AC2+ BC2 = AB2
nên AC2 = AB2+BC2
Suy ra LAD = √15 ≈ 3.8
Bài 56:
a) Ta có 92 = 81,152 = 225, 122 =144.
mà 225=81+144
hay 152=92+122.
Nên Δ có độ dài ba cạnh 9cm,15cm,12cm là Δ vuông.
b) Ta có 52=25,132=169,122=144.
Mà 169=25+144 nên Δ có độ dài ba cạnh 5dm, 13dm,12dm là Δvuông
c) Ta có 72=49, 102=100
vậy 72+ 72 ≠102
72+102 ≠72
Nên Δ có độ dài 3 canh là 7dm,7dm,10dm không phải là Δvuông
giúp mình làm bài 1 trang 115 sgk lớp 5 với
IC
3
4 tháng 6 2021
1. wife
2. lazy
3. shoes
4. invitation
5. women
6. expensive
7. sad
8. light
H
30 tháng 4 2021
Câu 6.6 trang 19 Sách Bài Tập SBT Toán lớp 7 tập 1
Tính M=820+420425+645M=820+420425+645.
Giải
M=820+420425+645=(23)20+(22)20(22)25+(26)5M=820+420425+645=(23)20+(22)20(22)25+(26)5
=260+240250+230=240(220+1)230(220+1)=210=1024.=260+240250+230=240(220+1)230(220+1)=210=1024.
Câu 6.7 trang 19 Sách Bài Tập SBT Toán lớp 7 tập 1
Tìm x, biết:
a) (x4)2=x12x5(x≠0);(x4)2=x12x5(x≠0);
b) x10 = 25x8.
Giải
a) (x4)2=x12x5(x≠0)⇒x8=x7(x4)2=x12x5(x≠0)⇒x8=x7
⇒x8−x7=0⇒x7.(x−1)=0⇒x8−x7=0⇒x7.(x−1)=0
⇒x−1=0⇒x−1=0 (vì x7 ≠ 0)
Vậy x = 1.
b) x10=25x8⇒x10−25x8=0⇒x8.(x2−25)=0x10=25x8⇒x10−25x8=0⇒x8.(x2−25)=0
Suy ra x8 = 0 hoặc x2 - 25 = 0.
Do đó x = 0 hoặc x = 5 hoặc x = -5.
Vậy x∈{0;5;−5}x∈{0;5;−5}.
Câu 6.8 trang 19 Sách Bài Tập SBT Toán lớp 7 tập 1
Tìm x, biết:
a) (2x+3)2=9121(2x+3)2=9121;
b) (3x−1)3=−827(3x−1)3=−827
Giải
a) (2x+3)2=9121=(±311)2(2x+3)2=9121=(±311)2
Nếu 2x+3=311⇒x=−15112x+3=311⇒x=−1511
Nếu 2x+3=−311⇒x=−18112x+3=−311⇒x=−1811
b) (3x−1)3=−827=(−23)3(3x−1)3=−827=(−23)3
⇔3x−1=−23⇔x=19
a/\(Vì\frac{1}{9}=\frac{2}{18}=\frac{3}{27}=\frac{4}{36}=\frac{5}{45}\)
Nên x và y là 2 đại lượng tỉ lệ thuận .
b/Ta có \(\frac{6}{72}\ne\frac{9}{90}\)
Nên x và y là 2 đại lượng không tỉ lệ thuận .