Cho tam giác ABC= tam giác GIK và IG:IK:KG=2:3:4
Và chu vi của tam giác GIK=36cm .Tính các cạnh của tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
IG/2 = IK/3 = KG/4 và IG + IK + KG = 36
Áp dụng tính chất của dãy tỉ số bằng nhau, có:
\(\frac{IG}{2}=\frac{IK}{3}=\frac{KG}{4}=\frac{IG+IK+KG}{2+3+4}=\frac{36}{9}=4\)
Suy ra: \(\frac{IG}{2}=4\Rightarrow IG=4\cdot2=8\)
\(\frac{IK}{4}=4\Rightarrow IK=4\cdot4=16\)
\(\frac{KG}{4}=4\Rightarrow KG=4\cdot4=16\)
Mà tam giác ABC = tam giác GIK
=> AB = IG; BC = IK; AC = KG (các cặp cạnh tương ứng)
=> AB = IG = 8; BC = IK = 16; AC = KG = 16

Đặt AB=a; AC=b
Theo đề, ta có: a/3=b/4
Đặt a/3=b/4=k
=>a=3k; b=4k
Theo đề, ta có: 3k+4k+5k=36
=>12k=36
=>k=3
=>AB=9; AC=12; BC=15

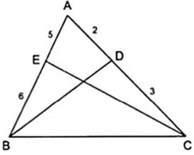
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
+ AB/BC = AD/DC = 2/3 = 4/6
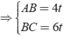 với t > 0
với t > 0
+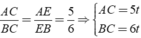
Theo giả thiết ta có: P A B C = A B + A C + B C = 15 t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )

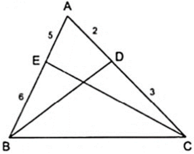
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
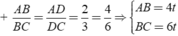 với t > 0
với t > 0
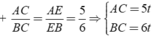
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )

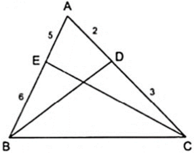
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
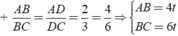 với t > 0
với t > 0
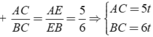
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )

6.)
Khi 2 tam giác đồng dạng với nhau thì cạnh nhỏ nhất của tam giác này sẽ tương ứng với cạnh nhỏ nhất của tam giác kia.
Theo đề:\(A'B'\)=4,5
Ta có:\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(\Rightarrow\)\(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow\)\(B'C'=7,5cm,C'A'=10,5cm\)