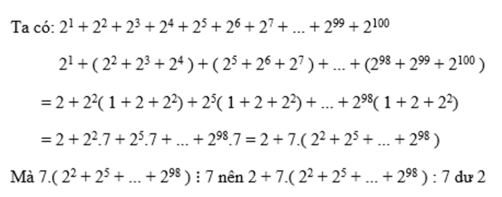tìm số n biết : 2n - 1 - 2 - 21 - 22 - 23 - .......... - 2100 = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(21+22+23+...+n+4840\)
\(\Rightarrow\left[\left(n-21\right):1+1\right]\left(n+21\right):2=4840\)
\(\Rightarrow\left(n-20\right)\left(n+21\right)=9680\)
\(\Rightarrow n^2+n-420=9680\)
\(\Leftrightarrow n^2+n-100100=0\)
\(\Leftrightarrow n^2-100n+101n-100100=0\)
\(\Leftrightarrow n\left(n-100\right)+101\left(n-100\right)=0\)
\(\Leftrightarrow\left(n+101\right)\left(n-100\right)=0\)
\(\Leftrightarrow\left[n=-101\text{(loại)},n=100\right]\)
\(\Rightarrow n=100\)
\(\text{Hok tốt!}\)
\(\text{@Kaito Kid}\)
21 + 22 + 23 + ... + n = 4840
=> [(n - 21) : 1 + 1](n + 21) : 2 = 4840
=> (n - 20)(n + 21) = 9680
=> n2 + n - 420 = 9680
<=> n2 + n - 10100 = 0
<=> n2 - 100n + 101n - 10100 = 0
<=> n(n - 100) + 101(n - 100) = 0
<=> (n + 101)(n - 100) = 0
<=> \(\orbr{\begin{cases}n=-101\left(\text{loại}\right)\\n=100\end{cases}}\)
Vậy n = 100


Ta có
2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100
= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )
= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2
= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98
Mà 7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7
Nên 2 + 7 2 2 + 2 5 + . . . + 2 98 : 7 d ư 2

Ta có A=20+21+22+23+...2100
2A=21+22+...+2101
2A-A=(21+22+...+2100)-(20+21+...+2100)
A=2101-1
Mà 2101-1=(........02)-1=........01 chia 100 dư 1
Chúc bạn học tốt.

\(A=1+2+2^2+2^3+...+2^{100}\)
\(=1+\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{99}+2^{100}\right)\)
\(=1+2\left(1+2\right)+2^3\left(1+2\right)+...+2^{99}\left(1+2\right)\)
\(=1+3\left(2+2^3+...+2^{99}\right)\)
=>A chia 3 dư 1

Đặt A = \(1+2+2^2+2^3+2^4+....+2^{100}\)
2A = \(2\left(1+2+2^2+2^3+2^4+....+2^{100}\right)\)
= \(2+2^2+2^3+2^4+2^5+...+2^{101}\)
2A - A = \(\left(2+2^2+2^3+2^4+2^5+....+2^{101}\right)-\left(1+2^2+2^3+2^4+...+2^{100}\right)\)
= \(2^{101}-1\)