cho tam giác ANC cân tại A có BC = 6cm, đg cao AH = 4cm.tính đg cao ứng vs cạnh bên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2023
ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AB^2=3^2+4^2=25\)
=>AB=5(cm)
Xét ΔAHB vuông tại H có
\(sinB=\dfrac{AH}{AB}=\dfrac{4}{5}\)
\(cosB=\dfrac{BH}{AB}=\dfrac{3}{5}\)
\(tanB=\dfrac{AH}{BH}=\dfrac{4}{3}\)
\(cotB=\dfrac{BH}{AH}=\dfrac{3}{4}\)
1 tháng 7 2023
a: Gọi giao của AH với BC là M
=>AH vuông góc BC tại M
góc AFH=góc AEH=90 độ
=>AEHF nội tiếp đường tròn đường kính AH
=>IF=IA=IE=IH
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp đường tròn đường kính BC
=>KF=KE=KB=KC
góc IFH+góc KFH
=góc IHF+góc KCH
=góc KCH+90 độ-góc KCH=90 độ
=>FK vuông góc FI
b: FI=AH/2=3cm
FK=BC/2=4cm
=>IK=căn 3^2+4^2=5cm
21 tháng 7 2018
2) A B C D
ÁP dụng định lí pitago ta có
\(AB=\sqrt{BD^2-DA^2}\)
\(=\sqrt{\sqrt{10}^2-1}=3cm\)
áp dụng hàm sin ta có
\(sin\left(\widehat{ABD}\right)=\frac{AD}{BD}\Leftrightarrow sin\left(X\right)=\frac{1}{\sqrt{10}}\)( shift slove )
\(\Rightarrow\widehat{ABD}\approx18,5^O\Rightarrow B=37^O\)
ÁP DỤNG HÀM COS TA CÓ
\(cos\left(B\right)=\frac{AB}{BC}=\frac{3}{BC}\Rightarrow BC=\frac{3}{cos\left(37\right)}\approx3,7cm\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=1,5\)
=> \(S_{ABC}=\frac{3\cdot1,5}{2}=2,25CM^2\)
Nghĩ sao làm vậy nên thông cảm ^_^ bạn có thể áp dụng cách này
21 tháng 7 2018
1. https://olm.vn/hoi-dap/question/103400.html
Bạn tham khảo link này nhé
30 tháng 3 2023
a: Xét ΔHAB vuông tại H và ΔBAC vuôg tại B có
góc A chung
=>ΔHAB đồng dạng với ΔBAC
b: ΔBAC vuôngtại B có BH là đường cao
nên BH^2=AH*AC
20 tháng 6 2023
a: BH=CH=3cm
=>AB=AC=5cm
AB=AC<BC
=>góc B=góc C<góc A
b: O nằm trên trung trực của AB,AC
=>OA=OB=OC
=>O nằm trên trung trực của BC
=>A,O,H thẳng hàng
14 tháng 11 2021
Gọi đường cao tương ứng cạnh AC là BK
Vì AH là đg cao tam giác ABC cân nên AH cũng là trung tuyến
\(\Rightarrow CH=\dfrac{1}{2}BC=3\left(cm\right)\)
Áp dụng PTG: \(AC=\sqrt{AH^2+CH^2}=5\left(cm\right)\)
Lại có \(S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}BK\cdot AC\)
\(\Rightarrow BK=\dfrac{AH\cdot BC}{AC}=\dfrac{4\cdot6}{5}=2,4\left(cm\right)\)
CM
19 tháng 1 2017
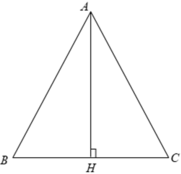
Xét Δ ABC cân tại A có BC = 30( cm )
⇒ BH = CH = 15( cm ).
Áp dụng đinh lý Py – ta – go ta có:
tam giác ABC