Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho tam giác ABC vuông tại A .Biết AB=7cm và AC=21 cm .tính các tỉ số lượng giác của góc B vá góc C

ABC cân tại A nên H đồng thời là trung điểm BC
\(\Rightarrow BH=CH=6\left(cm\right)\)
Trong tam giác vuông ABH:
\(AB=\sqrt{AH^2+BH^2}=2\sqrt{13}\)
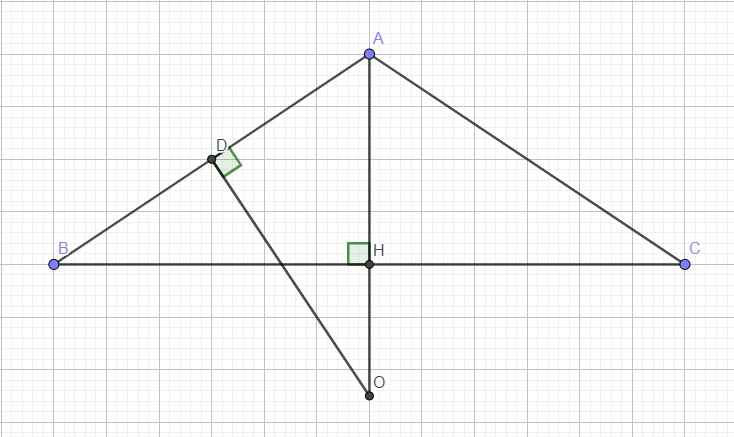
Gọi D là trung điểm AB, qua D kẻ đường trung trực AB, kéo dài cắt AH tại O
\(\Rightarrow\) O là tâm đường tròn ngoại tiếp tam giác \(\Rightarrow OA=R\)
\(AD=\dfrac{1}{2}AB=\sqrt{13}\)
Trong tam giác vuông ABH: \(cos\widehat{BAH}=\dfrac{AH}{AB}\)
Trong tam giác vuông ADO: \(cos\widehat{BAH}=\dfrac{AD}{AO}\)
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{AD}{AO}\Rightarrow R=AO=\dfrac{AB.AD}{AH}=6,5\left(cm\right)\)

Vì \(\widehat{B}=120^0\) nên đường cao AH ứng với cạnh BC sẽ nằm ngoài tam giác ABC
Ta có: \(\widehat{ABH}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{ABH}+120^0=180^0\)
hay \(\widehat{ABH}=60^0\)
Xét ΔABH vuông tại H có
\(\widehat{ABH}=60^0\)(cmt)
nên \(\sin\widehat{ABH}=\dfrac{\sqrt{3}}{2}\); \(\cos\widehat{ABH}=\dfrac{1}{2}\); \(\tan\widehat{ABH}=\sqrt{3}\); \(\cot\widehat{ABH}=\dfrac{\sqrt{3}}{3}\)
Xét ΔABH vuông tại H có
\(\widehat{BAH}=30^0\)
nên \(\sin\widehat{BAH}=\dfrac{1}{2}\); \(\cos\widehat{BAH}=\dfrac{\sqrt{3}}{2}\); \(\tan\widehat{BAH}=\dfrac{\sqrt{3}}{3}\); \(\cot\widehat{BAH}=\sqrt{3}\)

A B C H
a) \(BC=BH+HC=2+6=8\)
Áp dụng hệ thức lượng ta có:
\(AH^2=BH.HC\)
\(\Rightarrow\)\(AH^2=2.6=12\)
\(\Rightarrow\)\(AH=\sqrt{12}=2\sqrt{3}\)
\(AB^2=BH.BC\)
\(\Rightarrow\)\(AB^2=2.8=16\)
\(\Rightarrow\)\(AB=4\)
\(AC^2=HC.BC\)
\(\Rightarrow\)\(AC^2=6.8=48\)
\(\Rightarrow\)\(AC=4\sqrt{3}\)
b) \(sinB=\frac{AH}{AB}=\frac{2\sqrt{3}}{4}=\frac{\sqrt{3}}{2}\)
\(cosB=\frac{BH}{AB}=\frac{2}{4}=\frac{1}{2}\)
\(tanB=\frac{AH}{BH}=\frac{2\sqrt{3}}{2}=\sqrt{3}\)
\(cotB=\frac{BH}{AH}=\frac{2}{2\sqrt{3}}=\frac{1}{\sqrt{3}}\)

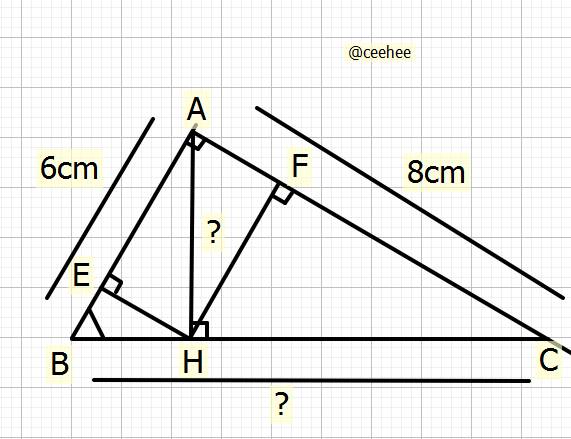
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)
ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AB^2=3^2+4^2=25\)
=>AB=5(cm)
Xét ΔAHB vuông tại H có
\(sinB=\dfrac{AH}{AB}=\dfrac{4}{5}\)
\(cosB=\dfrac{BH}{AB}=\dfrac{3}{5}\)
\(tanB=\dfrac{AH}{BH}=\dfrac{4}{3}\)
\(cotB=\dfrac{BH}{AH}=\dfrac{3}{4}\)