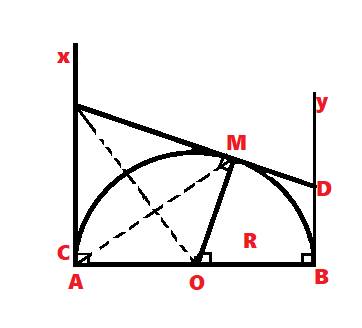
cho đường tròn O đường kính AB. vẽ 2 tiếp tuyến Ax, By. trên Ax lấy D, By lấy E sao cho DE là tiếp tuyến của đường tròn. CM \(\frac{1}{2}\)> r/R > \(\frac{1}{3}\)( r là bán kính đường tròn nội tiếp tam giác ODE, R là bán kính đường tròn tâm O đường kính AB đã cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 12 2023
a: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM và OC là phân giác của \(\widehat{MOA}\)
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
CA=CM
=>C nằm trên đường trung trực của AM(1)
OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OC là đường trung trực của AM
=>OC\(\perp\)AM
b: Xét tứ giác CAOM có \(\widehat{CAO}+\widehat{CMO}=90^0+90^0=180^0\)
nên CAOM là tứ giác nội tiếp
=>C,A,O,M cùng thuộc một đường tròn
c: Xét (O) có
DM,DB là tiếp tuyến
Do đó: OD là phân giác của góc MOB và DM=DB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
\(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
=>ΔCOD vuông tại O
Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
mà MC=CA và DM=DB
nên \(CA\cdot DB=OM^2=R^2\)