Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời hộ mình cái xin. mình đã 2 năm ko on r giờ mới on lại :(((.Xin mọi người trả lời giúp mình :(((

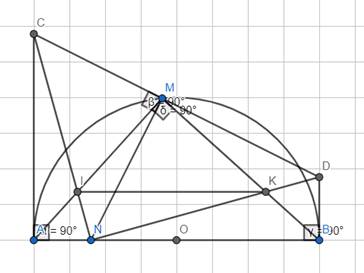
△AMB nội tiếp đường tròn đường kính AB nên △AMB vuông tại M.
- Ta có: \(\widehat{CAB}+\widehat{DBA}=90^0+90^0=180^0\)
\(\Rightarrow\widehat{CAM}+\widehat{MAB}+\widehat{DBM}+\widehat{MBA}=180^0\)
\(\Rightarrow\left(\widehat{CAM}+\widehat{DBM}\right)+\left(\widehat{MAB}+\widehat{MBA}\right)=180^0\)
\(\Rightarrow\left(\widehat{CAM}+\widehat{DBM}\right)+90^0=180^0\) nên \(\widehat{CAM}+\widehat{DBM}=90^0\)
Tứ giác ANMC có: \(\widehat{NAC}+\widehat{NMC}=90^0+90^0=180^0\)
Nên tứ giác ANMC nội tiếp \(\Rightarrow\widehat{CAM}=\widehat{CNM}\)
Tứ giác BNMD có: \(\widehat{NBD}+\widehat{NMD}=90^0+90^0=180^0\)
\(\Rightarrow\)Tứ giác BNMD nội tiếp \(\Rightarrow\widehat{MBD}=\widehat{MND}\)
\(\Rightarrow\widehat{CNM}+\widehat{MND}=\widehat{CAM}+\widehat{MBD}=90^0\)
\(\Rightarrow\widehat{INK}=90^0\).
Tứ giác MINK có: \(\widehat{IMK}+\widehat{INK}=90^0+90^0=180^0\)
\(\Rightarrow\)Tứ giác MINK nội tiếp nên \(\widehat{MIK}=\widehat{MNK}\)
Lại có \(\widehat{MNK}=\widehat{MBD}\left(cmt\right)\) \(\Rightarrow\widehat{MIK}=\widehat{MBD}\)
Xét (O): \(\widehat{MBD}=\widehat{MAB}\left(=\dfrac{1}{2}sđ\stackrel\frown{MB}\right)\)
\(\Rightarrow\widehat{MIK}=\widehat{MAB}\) nên IK//AB

ΔKBO=ΔKCO
=>KB=KC
=>KO là trung trực của BC
ΔKCO đồng dạng với ΔCIO
=>OC/OI=OK/OC
=>OC^2=OI*OK
=>OI*OK=ON^2
=>OI/ON=ON/OK
=>ΔOIN đồng dạng với ΔONK
=>gócc ONI=góc OKN
Tương tự, ta có: OI/OM=OM/OK
=>ΔMKO đồng dạng với ΔIMO
=>góc MKO=góc IMO=góc INO
=>góc MKD=góc NKD
=>K,M,N thẳng hàng
=>K luôn thuộc MN

trên CD lấy điểm N, kẻ MN vuông góc với CD
=> 2 tam giac vuông MBC=MNC
=> 2tam giác MAD=MND
=> MB=MN=MA = R
vậy CD là tiếp tuyến đường tròn tâm M

Ta có: \(OD//O'B\left(\perp AB\right)\)
\(\Rightarrow\frac{AO}{AO'}=\frac{OD}{O'B}=\frac{R}{R'}=\frac{OI}{O'M}=\frac{OI}{O'I}\)
OI cắt O’I và A, I, M thẳng hàng ( gt ) nên suy ra OI // O’M \(\Rightarrow\widehat{DOI}=\widehat{BO'M}\)
Mà \(\widehat{BDI}=\frac{1}{2}\widehat{DOI}=\frac{1}{2}\)sđ cung DI và \(\widehat{BIM}=\frac{1}{2}\widehat{BO'M}=\frac{1}{2}\)sđ cung \(BM\Rightarrow\widehat{BDI}=\widehat{BIM}\)
Nên AM là tiếp tuyến của đường tròn ngoại tiếp của tam giác BDI ( đpcm )