Tìm tất cả các giá trị của tham số m để hàm số \(y=x^4-2\left(m+1\right)x^2+m^2-1\) đạt cực tiểu tại x=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
CH
2

10 tháng 8 2021
Tìm tất cả các giá trị nguyên của m để hàm số y=x^8+(m-2)x^5-(m^2-4)x^4+1 đạt cực tiểu tại x=0.
m= 2
nha bạn
bạn muốn tl rõ hơn thì bạn tìm trên google

NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
\(y'=4x^3+12mx^2+6\left(m+1\right)x=2x\left[2x^2+6mx+3\left(m+1\right)\right]\)
Hàm có cực tiểu mà ko có cực đại khi và chỉ khi \(y'=0\) có đúng 1 nghiệm đơn
TH1: \(2x^2+6mx+3\left(m+1\right)=0\) có nghiệm \(x=0\)
\(\Leftrightarrow m=-1\)
TH2: \(2x^2+6mx+3\left(m+1\right)=0\) có ít hơn 2 nghiệm
\(\Leftrightarrow\Delta'=9m^2-6\left(m+1\right)\le0\)
\(\Leftrightarrow\dfrac{1-\sqrt{7}}{3}\le m\le\dfrac{1+\sqrt{7}}{3}\)
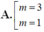
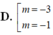
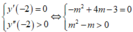
Hàm trùng phương \(y=ax^4+bx^2+c\) có hệ số \(a>0\) đạt cực tiểu tại \(x=0\) khi và chỉ khi \(a.b\ge0\)
\(\Rightarrow1.\left(-2\left(m+1\right)\right)\ge0\Rightarrow m+1\le0\Rightarrow m\le-1\)
bạn ơi, cô giáo mình giải bài này ra m=-1