Cho hàm số y= f(x)= 3x-4
a. Tìm tọa độ giao điểm của đồ thị hàm số với hai trục tọa dộ
b. Tính f(2), f(-1/2) ; \(f\left(\sqrt{7-\sqrt{24}}\right)\)
c. Các điểm sau có thuộc đồ thị hàm số không? A(1;-1) B(-1;1) C(2;10) D(-2;10)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 4 2021
Câu 2:
c) Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{1}{2}x^2=2x+6\)
\(\Leftrightarrow\dfrac{1}{2}x^2-2x-6=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow x^2-4x+4=16\)
\(\Leftrightarrow\left(x-2\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=4\\x-2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Thay x=6 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot6^2=18\)
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Vậy: Tọa độ giao điểm của (P) và (d) là (6;18) và (-2;2)
15 tháng 4 2021
Câu 3:
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{1}=2\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{-1}{1}=-1\end{matrix}\right.\)
Ta có: \(P=x_1^3+x_2^3\)
\(=\left(x_1+x_2\right)^3-3\cdot x_1x_2\left(x_1+x_2\right)\)
\(=2^3-3\cdot\left(-1\right)\cdot2\)
\(=8+3\cdot2\)
\(=8+6=14\)
Vậy: P=14
30 tháng 7 2023
1:
a: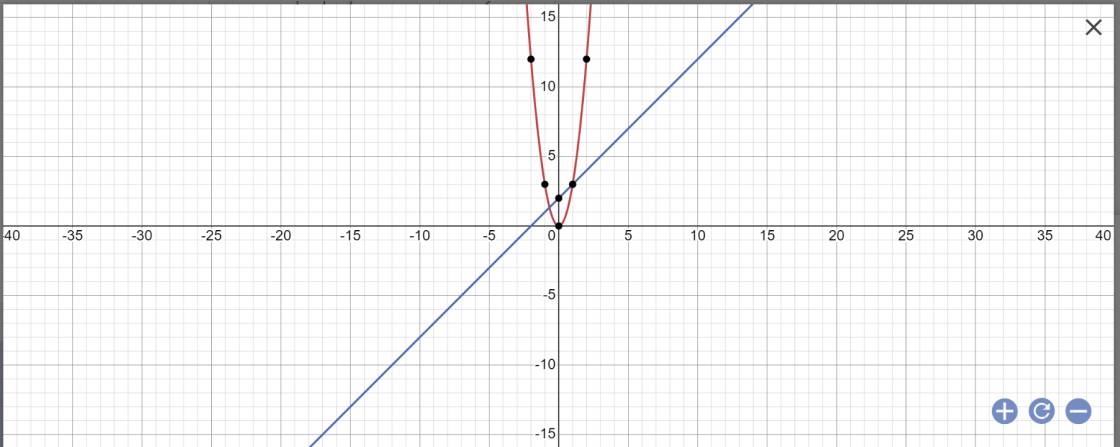 
b: PTHĐGĐ là:
3x^2-x-2=0
=>3x^2-3x+2x-2=0
=>(x-1)(3x+2)=0
=>x=1 hoặc x=-2/3
Khi x=1 thì y=3*1^2=3
Khi x=-2/3 thì y=3*4/9=4/3
c: f(-1)=3(-1)^2=3
f(2)=3*2^2=12
f(1/3)=3*(1/3)^2=1/3
)
10 tháng 2 2021
a) Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Ox là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-2x+1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+1=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x=-1\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của đồ thị hàm số y=-2x+1 với trục Oy là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
a: Tọa độ giao của (d) với trục ox là:
y=0 và 3x-4=0
=>x=4/3 và y=0
Tọa độ giao của (d) với trục Oy là:
x=0 và y=3*0-4=-4
b: \(f\left(2\right)=3\cdot2-4=2\)
f(-1/2)=-3/2-4=-11/2
\(f\left(\sqrt{7-\sqrt{24}}\right)=f\left(\sqrt{6}-1\right)=3\sqrt{6}-3-4=3\sqrt{6}-7\)
c: \(f\left(1\right)=3\cdot1-4=-1=y_A\)
=>A thuộc đồ thị
\(f\left(-1\right)=-3-4=-7< >1\)
=>B ko thuộc đồ thị
f(2)=3*2-4=6-4=2<>10
=>C ko thuộc đồ thị
f(-2)=-6-4=-10<>10
=>D ko thuộc đồ thị