Nhờ các bạn và mọi người giải giúp mình bài bất đẳng thức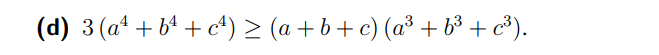
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PK
0
Những câu hỏi liên quan
NT
0
TH
2
17 tháng 4 2019
\(\frac{2}{5}-\frac{1}{7}+\frac{3}{5}.\frac{1}{3}=\frac{14}{35}-\frac{5}{35}+\frac{7}{35}=\frac{16}{35}\)
17 tháng 4 2019
\(\frac{2}{5}-\frac{1}{7}+\frac{3}{5}\times\frac{1}{3}\)
\(=\frac{2}{5}-\frac{1}{7}+\frac{1}{5}\)
\(=\frac{9}{35}+\frac{1}{5}\)
\(=\frac{16}{35}\)
DM
Tìm các số a,b,c thỏa mãn các bất đẳng thức: lal<lb-cl,lbl<la-cl,lcl<la-bl
Các bạn giải giúp mình nhé
0
AH
Akai Haruma
Giáo viên
29 tháng 5 2021
Bài 1:
Vì $a\geq 1$ nên:
\(a+\sqrt{a^2-2a+5}+\sqrt{a-1}=a+\sqrt{(a-1)^2+4}+\sqrt{a-1}\)
\(\geq 1+\sqrt{4}+0=3\)
Ta có đpcm
Dấu "=" xảy ra khi $a=1$
AH
Akai Haruma
Giáo viên
29 tháng 5 2021
Bài 2:
ĐKXĐ: x\geq -3$
Xét hàm:
\(f(x)=x(x^2-3x+3)+\sqrt{x+3}-3\)
\(f'(x)=3x^2-6x+3+\frac{1}{2\sqrt{x+3}}=3(x-1)^2+\frac{1}{2\sqrt{x+3}}>0, \forall x\geq -3\)
Do đó $f(x)$ đồng biến trên TXĐ
\(\Rightarrow f(x)=0\) có nghiệm duy nhất
Dễ thấy pt có nghiệm $x=1$ nên đây chính là nghiệm duy nhất.
25 tháng 7 2019
Cho x,y>0 thỏa mãn x3+y3=x−y. Chứng minh: x2+y2<1.
Cho x,y>0x,y>0 thỏa mãn x3+y3=x−y. Chứng minh: x2+y2<1.
.............................