Cho nửa đường tròn (O), đường kính AB = 2R, d là tiếp tuyến của (O) tại B. Lấy M bất kì trên nửa đường tròn, tia AM cắt d tại N. Gọi C là trung điểm của AM, tia CO cắt d tại D
Chứng minh: a) NO vuông góc AD
b) CA.CN = CD.CO
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: ΔOAM cân tại O
mà OC là trung tuyến
nên OC vuông góc AM
góc OBN+góc OCN=180 độ
=>OCNB nội tiếp
2: Xét ΔACO vuông tại C và ΔABN vuông tại B có
góc CAO chung
=>ΔACO đồng dạng với ΔABN
=>AC/AB=AO/AN
=>AC*AN=AO*AB

a) OBNC có NCO=OBN=90 nên OBNC là tứ giác nội tiếp
b) Xét tam giác ADC có AB,DC là các đường cao
mà AB cắt DC tại O
suy ra O là trực tâm của tam giác ADC
nên NO vuông góc với AD
c)
CONB là tứ giác nôi tiếp nên COA=CNB
Xét tam giác ACO và tam giác DCN
COA=CNB(cmt)
ACO=NCD=90
nên tam giác ACO đồng dạng với tam giác DNC
nên CA.CN=CO.CD
Còn câu d mk chịu

AB cắt đường tròn ngoại tiếp tam giác AEK tại D
Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle EMB+\angle EHB=90+90=180\)
\(\Rightarrow EMBH\) nội tiếp \(\Rightarrow\angle KBD=\angle MBH=\angle AEH\)
Vì KEAD nội tiếp \(\Rightarrow\angle AEH=\angle KDB\Rightarrow\angle KBD=\angle KDB\)
\(\Rightarrow\Delta KDB\) cân tại K có KH là đường cao
\(\Rightarrow H\) là trung điểm BD mà B,H cố định \(\Rightarrow D\) cố định
Vì KEAD nội tiếp \(\Rightarrow I\in\) trung trực AD mà A,D cố định
\(\Rightarrow\) đpcm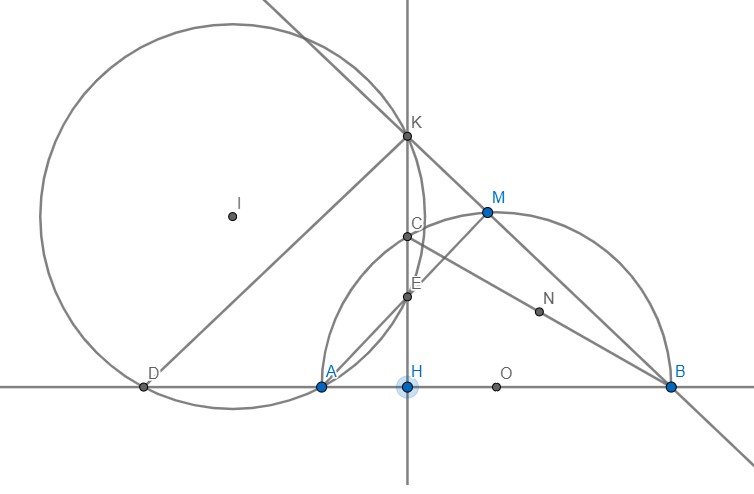


a) \(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat{ACB}=90^o\). Vậy tam giác ABC vuông tại C.
Xét tam giác vuông PAB có đường cao AC, áo dụng hệ thức lượng trong tam giác ta có:
\(PA^2=PC.PB\)
b) Áp dụng tính chất hai tiếp tuyến cắt nhau, ta có PA = PM
Lại có OA = OM nên PO là trung trực của AM.
c) Ta có \(\widehat{CBA}=30^o\Rightarrow\widehat{CAB}=60^o\) hay tam giác CAO đều. Suy ra AC = R
Xét tam giác vuông PAB có đường cao AC, áo dụng hệ thức lượng trong tam giác ta có:
\(\frac{1}{AC^2}=\frac{1}{AP^2}+\frac{1}{AB^2}\Rightarrow\frac{1}{R^2}=\frac{1}{AP^2}+\frac{1}{4R^2}\)
\(\Rightarrow AP=\frac{2R}{\sqrt{3}}\)
\(\Rightarrow PO=\sqrt{PA^2+AO^2}=\frac{\sqrt{21}R}{3}\)
Xét tam giác vuông PAO, đường cao AN, áo dụng hệ thức lượng ta có:
\(\frac{1}{AN^2}=\frac{1}{PA^2}+\frac{1}{AO^2}\Rightarrow AN=\frac{2\sqrt{7}R}{7}\)
\(\Rightarrow AM=2AN=\frac{4\sqrt{7}}{7}R\)
d) Kéo dài MB cắt AP tại E.
Ta thấy ngay tam giác EMA vuông có PM = PA nên PA = PE
Do MH // AE nên áo dụng định lý Ta let ta có:
\(\frac{HI}{AP}=\frac{IB}{PB}=\frac{MI}{EP}\)
Do AP = EP nên MI = HI
Ta cũng có N là trung điểm AM nên NI là đường trung bình tam giác AMH.
\(\Rightarrow NI=\frac{AH}{2}\)
Xét tam giác vuông AMB, đường cao MH, áp dụng hệ thức lượng ta có:
\(AH.AB=AM^2\Rightarrow AH=\frac{8}{7}R\)
\(\Rightarrow NI=\frac{4}{7}R\)