Tìm n\(\in\)\(ℕ\)biết:
n2 + n + 1 \(⋮\)n + 2; n > 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
2
H
3 tháng 6 2021
n2 + n + 4 = n(n + 1) + 4 chia hết cho n + 1
Suy ra :
4 chia hết cho n + 1
Vậy : n + 1 ∈ Ư(4) = {-1;1;-2;2;-4;4}
Với n + 1 = - 1 <=> n = -2
Với n + 1 = 1 <=> n = 0
Với n + 1 = -2 <=> n = -3
Với n + 1 = 2 <=> n = 1
Với n + 1 = -4 <=> n = -5
Với n + 1 = 4 <=> n = 3
HX
1
YN
13 tháng 2 2023
Xét các trường hợp:
\(n=1\Leftrightarrow1!=1=1^2\) là số chính phương
\(n=2\Leftrightarrow1!+2!=3\) không phải là số chính phương
\(n=3\Leftrightarrow1!+2!+3!=9=3^3\) là số chính phương
\(n\ge4\Leftrightarrow1!+2!+3!+4!=33\) còn \(5!,6!,7!,...,n!\) đều có tận cùng là \(0\Rightarrow1!+2!+3!+...+n!\) có tận cùng là chữ số 3 nên không phải là số chính phương
Vậy \(n\in\left\{1;3\right\}\).
ND
0
CM
2 tháng 5 2017
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Tách. Bước 2. Áp dụng tính chất chia hết của một tổng. Bước 3. Tìm n+1. Bước 4. Tìm n. |
Ta có: 3 n + 4 = 3 n + 3 + 1 = 3 n + 1 + 1 Để 3 n + 4 ⋮ n + 1 thì 1 ⋮ n + 1 ⇒ n + 1 = 1 ⇒ n = 0 |
CM
1 tháng 4 2017
Chọn đáp án D
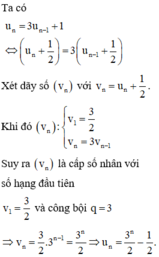
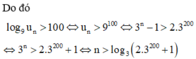
Vậy số tự nhiên n nhỏ nhất thỏa mãn điều kiện trên là n 0 = 201
HM
5 tháng 10 2023
không nhé, vì từ 5! trở đi sẽ chia hết cho 5 (vì 1x2x3x4x5x.... (chia hết cho 5))
Đặt phần từ 5! -> 2023! = b (b chia hết cho 5)
ta còn: 1!+2!+3!+4!+b
=1+1x2+1x2x3 + 1x2x3x4 + b
=1+2+6+24+b
=33+b
mà 33 không chia hết cho 5 trong khi b chia hết cho 5
=> S không chia hết cho 5
\(n^2+n+1⋮n+2\)\(\Rightarrow n^2+2n-n+1⋮n+2\Rightarrow n-1⋮n+2\Rightarrow n+2-3⋮n+2\)
đến đây 3 chia het cho n+2 suy ra n+2 thuoc uoc cua 3. bạn tính đc các giá trị thỏa mãn điều kiện n thuộc số tự nhiên và lớn hơn 0 đó là n=1
Cảm ơn nha!