B=1+41+42+43+.................+4n [n>2;n thuộc N]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DK
2
LM
Lê Minh Vũ
CTVHS
13 tháng 6 2023
Dãy trên có số số hạng là:
( 100 - 41 ) : 1 + 1 = 60 ( số hạng )
Tổng của dãy trên là:
( 100 + 41 ) x 60 : 2 = 4230
DC
2
6 tháng 5 2017
ta thấy \(\frac{1}{41}< \frac{1}{40};\frac{1}{42}< \frac{1}{40};\frac{1}{43}< \frac{1}{40};...;\frac{1}{60}< \frac{1}{40}\)
\(\Rightarrow\frac{1}{41}+\frac{1}{42}+\frac{1}{43}+...+\frac{1}{60}< \frac{1}{40}+\frac{1}{40}+\frac{1}{40}+...+\frac{1}{40}=\frac{1}{40}.20=\frac{20}{40}=\frac{1}{2}\)
\(\Rightarrow B< \frac{1}{2}\)( đpcm )
NK
2
26 tháng 1 2019
\(\frac{1}{2}+\frac{5}{6}+\frac{11}{12}+\frac{19}{20}+\frac{29}{30}+\frac{41}{42}+\frac{42}{43}\)
\(=1-\frac{1}{2}+1-\frac{1}{6}+1-\frac{1}{12}+1-\frac{1}{20}+1-\frac{1}{30}+1-\frac{1}{42}+\frac{42}{43}\)
\(=6-\left(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}\right)+\frac{42}{43}\)
\(=6-\left(\frac{1}{1x2}+\frac{1}{2x3}+\frac{1}{3x4}+\frac{1}{4x5}+\frac{1}{5x6}\right)+\frac{42}{43}\)
\(=6-\left(1-\frac{1}{6}\right)+\frac{42}{43}\)
...
bn tự tính tiếp nha
LT
0
HN
0
DT
Dang Tung
CTVHS
19 tháng 10 2023
B = (4^1 + 4^2) + (4^3 +4^4) + ... + (4^299 + 4^300)
= 4(1+4)+4^3(1+4)+...+4^299(1+4)
= 4.5+4^3 .5 +...+4^299. 5
= 5.(4+4^3+...+4^299) chia hết cho 5
T
19 tháng 10 2023
\(B=4^1+4^2+4^3+4^3+...+4^{300}\\=(4+4^2)+(4^3+4^4)+(4^5+4^6)+...+(4^{299}+4^{300})\\=4\cdot(1+4)+4^3\cdot(1+4)+4^5\cdot(1+4)+...+4^{299}\cdot(1+4)\\=4\cdot5+4^3\cdot5+4^5\cdot5+...+4^{299}\cdot5\\=5\cdot(4+4^3+4^5+...+4^{299})\)
Vì \(5\cdot(4+4^3+4^5+...+4^{299}) \vdots 5\)
nên \(B \vdots 5\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 giờ trước (9:05)
Olm chào em, em làm như này là cưa đúng rồi, em nhé.
HC
0
PP
0
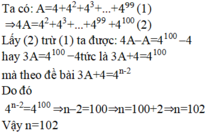
Ta có :
\(B=1+4^1+4^2+4^3+....+4^n\)
\(4B=4^1+4^2+4^3+4^4+...+4^{n+1}\)
\(4B-B=4^{n+1}-1\)
\(3B=4^{n+1}-1\)
\(B=\frac{4^{n+1}-1}{3}\)