A = {10;12;14;...;10000}
tìm số phần tử của A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PM
1
DM
2 tháng 3 2017
Theo đề bài ta có :
\(a^n=a^{10}\cdot\left(a^2\right)^{10}\cdot\left(a^3\right)^{10}...\left(a^{10}\right)^{10}\)
\(\Leftrightarrow a^n=a^{10}\cdot a^{20}\cdot a^{30}...a^{100}\)
\(\Rightarrow a^n=a^{10+20+30+...+100}\)
\(\Rightarrow n=10+20+30+...+100\)
\(\Rightarrow n=550\)
Đáp số : n = 550.
NH
1
KL
20 tháng 8 2016
Đặt A=1010+10102+...+10102015A=1010+10102+...+10102015
Dễ thấy 1010≡4(mod7)1010≡4(mod7)
Nên A≡4+410+4102+...+4102014A≡4+410+4102+...+4102014
Dễ chứng minh được 410≡4(mod7)410≡4(mod7)
Nên 410≡4102≡...≡4102015≡4(mod7)410≡4102≡...≡4102015≡4(mod7)
Do đó A≡4.2015≡3(mod7)A≡4.2015≡3(mod7)
AH
Akai Haruma
Giáo viên
15 tháng 7 2023
Lời giải:
a. $=2^8$
b. $=10^5$
c. $=8^3.6^3.7^3=(8.6.7)^3=336^3$
d. $=a^9$
e. $=10000.10^3.100=10^4.10^3.10^2=10^{4+3+2}=10^9$
f. $=(2x)^5$
15 tháng 7 2023
Bài \(2\)
\(a)\) \(2.2.2.2.2.2.2.2=2^8\)
\(b)\) \(10.10.10.10.10=10^5\)
\(c)\) \(8.8.8.6.6.7.7.7=8^3.6^2.7^3\)
\(d)\) \(a.a.a.a.a.a.a.a.a=a^9\)
\(e)\) \(10000 . 10 . 10 . 10 . 100\)
\(=10^4.10.10.10.10^2=10^9\)
\(f)\) \(2x.2x.2x.2x.2x=\left(2x\right)^5\)
12 tháng 10 2019
Mình làm câu a) nha!!!
+) \(A=2009^{2010}+2009^{2009}\)
\(=2009^{2009}.\left(2009+1\right)\)
\(=2009^{2009}.2010\)
+) \(B=2010^{2010}=2010^{2009}.2010\)
Vì \(2010^{2009}>2009^{2009}\)nên \(2010^{2009}.2010>2009^{2009}.2010\)hay \(B>A\)
Vậy \(A< B\)
Hok tốt nha^^
CM
15 tháng 1 2018
Điểm trung bình của xạ thủ A là:
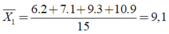
Điểm trung bình của xạ thủ B là:
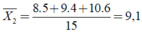
Chọn đáp án D.
LN
14 tháng 3 2017
Để (a+3)(a+10)<0 thì a+3 và a+10 trái dấu. Nên a+30 và a>-10. a+3<0 và a<-3. =>-10
So phan tu la
(10000 - 10) : 2 + 1 = 4996
Bài lúc nãy mình tính lộn đó bạn .
Số phần tử của A là :
( 10 000 - 10 ) : 1 + 1 = 9991 ( phần tử )
ĐS : 9991 phần tử