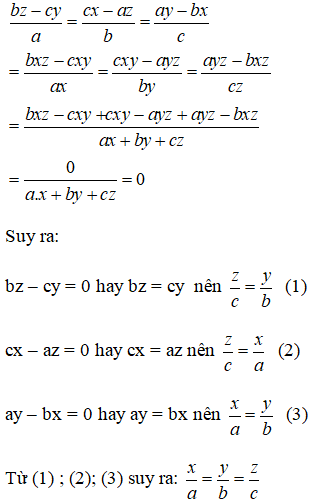tìm x,y,z biết \(\dfrac{xy}{ay+bx}=\dfrac{yz}{bz+cy}=\dfrac{xz}{cx+az}=\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\)(a,b,c là hằng số)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 11 2017
\(\dfrac{xy}{ay+bx}=\dfrac{yz}{bz+cy}=\dfrac{zx}{cx+az}=\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\left(1\right)\)
Ta có: \(\dfrac{xy}{ay+bx}=\dfrac{yz}{bz+cy}=\dfrac{zx}{cx+az}\)
\(\Rightarrow\dfrac{xyz}{ayz+bxz}=\dfrac{xyz}{bxz+cxy}=\dfrac{xyz}{cxy+ayz}\)
\(\Rightarrow ayz+bxz=bxz+cxy=cxy+ayz\)
\(\Rightarrow\left\{{}\begin{matrix}ayz+bxz=bxz+cxy\\ayz+bxz=cxy+ayz\\bxz+cxy=cxy+ayz\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}ayz=cxy\\bxz=cxy\\bxz=ayz\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}az=cx\\bz=cy\\bx=ay\end{matrix}\right.\left(2\right)\)
Thay (2) vào (1) ta có :
\(\dfrac{xy}{2ay}=\dfrac{yz}{2bz}=\dfrac{xz}{2cx}=\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\)
\(\Rightarrow\dfrac{x}{2a}=\dfrac{y}{2b}=\dfrac{z}{2c}=\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\left(3\right)\)
\(\Rightarrow\dfrac{x^2}{4a^2}=\dfrac{y^2}{4b^2}=\dfrac{z^2}{4c^2}=\dfrac{\left(x^2+y^2+z^2\right)^2}{\left(a^2+b^2+c^2\right)^2}=\)\(\dfrac{x^2+y^2+z^2}{4a^2+4b^2+4c^2}\)
\(\Rightarrow\dfrac{x^2+y^2+y^2}{a^2+b^2+c^2}=\dfrac{1}{4}\left(4\right).\)Thay (3) vào (2) ta có :
\(\dfrac{x}{2a}=\dfrac{y}{2b}=\dfrac{z}{2c}=\dfrac{1}{4}\Rightarrow\left\{{}\begin{matrix}x=\dfrac{a}{2}\\y=\dfrac{b}{2}\\z=\dfrac{c}{2}\end{matrix}\right.\)
NT
26 tháng 2 2018
Phương Ann Nhã Doanh đề bài khó wá Mashiro Shiina Đinh Đức Hùng
Nguyễn Huy Tú Lightning Farron Akai Haruma
AH
Akai Haruma
Giáo viên
10 tháng 9 2023
Lời giải:
Sửa đề: $z$ đầu tiên ở mẫu đổi thành $a$.
Ta có:
$\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}$
$=\frac{abz-cya}{a^2}=\frac{bcx-abz}{b^2}=\frac{acy-bcx}{c^2}$
$=\frac{abz-cya+bcx-abz+acy-bcx}{a^2+b^2+c^2}=\frac{0}{a^2+b^2+c^2}=0$
$\Rightarrow bz-cy=cx-az=ay-bx=0$
$\Rightarrow bz=cy; cx=az; ay=bx$
$\Rightarrow \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$
Ta có đpcm.
BM
8 tháng 8 2021
Ta có :
\(\dfrac{cy-bx}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}=\dfrac{bxz-cxy+cxy-ayz+ayz-bxz}{ax+by+cz}=0\)
\(\Rightarrow\dfrac{cy-bz}{x}=0\) \(\Rightarrow cy=bz\) \(\Rightarrow\) \(\dfrac{b}{y}=\dfrac{c}{z}\left(1\right)\)
\(\Rightarrow\dfrac{az-cx}{y}=0\) \(\Rightarrow az=cx\) \(\Rightarrow\dfrac{a}{x}=\dfrac{c}{z}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
10 tháng 2 2023
Ta có : \(\dfrac{bz-cy}{a}\text{=}\dfrac{cx-az}{b}\text{=}\dfrac{ay-bx}{c}\)
\(\Rightarrow\dfrac{a\left(bz-cy\right)}{a^2}\text{=}\dfrac{b\left(cx-az\right)}{b^2}\text{=}\dfrac{c\left(ay-bx\right)}{c^2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\dfrac{a\left(bz-cy\right)}{a^2}\text{=}\dfrac{b\left(cx-az\right)}{b^2}\text{=}\dfrac{c\left(ay-bx\right)}{c^2}\text{=}\dfrac{abz-acy+bcz-baz+cay-cbx}{a^2+b^2+c^2}\text{=}0\)
\(\Rightarrow\dfrac{bz-cy}{a}\text{=}0\Rightarrow bz\text{=}cy\)
\(\Rightarrow\dfrac{b}{c}\text{=}\dfrac{y}{z}\left(1\right)\)
\(\dfrac{cx-az}{b}\text{=}0\Rightarrow cx\text{=}az\)
\(\Rightarrow\dfrac{c}{a}\text{=}\dfrac{z}{x}\left(2\right)\)
Từ (1) và (2):
\(\Rightarrow dpcm\)