Hãy tự kiểm chứng mệnh đề: Hau đương thẳng y= ax+b ( a khác 0) và y= a'x+b' ( a' khác 0) vuông góc với nhau chỉ khi a.a'= -1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x A = - 1 ⇒ y = - 3 ⇒ A - 1 ; - 3 x B = 0 ⇒ y B = 11 ⇒ B 0 ; 1
Vì đường thẳng y = 1 - 2 x 1 + 2 x đi qua hai điểm A và B nên ta có hệ:
a - 1 + b = - 3 a . 0 + b = 1 ⇔ a = 4 b = 1
Vậy a b = 4
Đáp án B

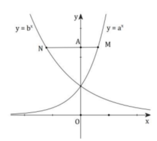
Gọi A(0;t) với t > 0. Suy ra 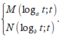
Theo giả thiết AN = 2AM nên suy ra
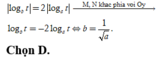

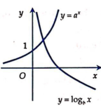
Đáp án A
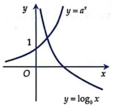
+ Từ đồ thị hàm số y = a x :Với x = 1 ⇒ a > 1
+ Từ đồ thị hàm số y = log b x :Với y = 1 ⇒ x < 1 có log b x = y ⇒ x = b y ⇒ 0 < b < 1

Chọn đáp án B
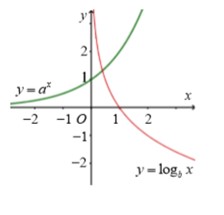
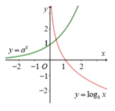
Ta thấy hàm số y = a x đồng biến trên ℝ nên a >1; hàm số y = log b x nghịch biến trên 0 ; + ∞ nên 0 <b <1
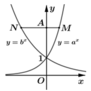
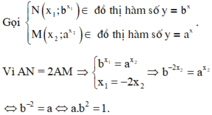
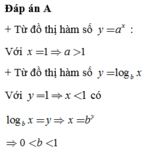


y=ax+b =>ax-y+b=0
=>VTPT là v=(a;-1)
y=a'x+b'
=>a'x+b'-y=0
=>VTPT là u=(a';1)
\(\overrightarrow{v}\cdot\overrightarrow{u}=a'\cdot a+1\cdot\left(-1\right)=1-1=0\)
=>Hai đường vuông góc