cho 2 điểm A và D và đường tròn (C) không đi qua A,D. một điểm B di chuyển trên (C). vẽ hình bình hành ABCD. tìm quỹ tích điểm C khi B di chuyển
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình nói sơ qua nhá:
a) Ta có ΔABO là Δ vuông tại B
Ta tính được AB=8 nhờ vào định lí Py-ta-go
b) Do I là trung điểm của CD nên OI⊥CD, lại suy ra được OI⊥IA
Nên I sẽ chuyển động trên đường tròn đường kính OA (cố định) khi C thay đổi trên đường tròn
c) Chứng minh cho ΔABD∼ΔACB
Suy ra được AC.AD=AB2 không đổi
tk nha bạn
thank you bạn
(^_^)

a) theo tính chất của hai tiếp tuyến cắt nhau , ta có :
AM = MB
Mà OA = OB ( = R )
\(\Rightarrow\)OM thuộc đường trung trực của AB
\(\Rightarrow\)OM \(\perp\)AB
b) Áp dụng hệ thức lượng vào \(\Delta AOM\),ta có :
\(OE.OM=OA^2=R^2\) ( không đổi i)
c) gọi F là giao điểm của AB với OH
Xét \(\Delta OEF\)và \(\Delta OHM\)có :
\(\widehat{HOE}\left(chung\right)\); \(\widehat{OEF}=\widehat{OHM}\left(=90^o\right)\)
\(\Rightarrow\Delta OEF~\Delta OHM\left(g.g\right)\)
\(\Rightarrow\frac{OE}{OH}=\frac{OF}{OM}\Rightarrow OF.OH=OE.OM=R^2\Rightarrow OF=\frac{R^2}{OH}\)
Do đường thẳng d cho trước nên OH không đổi
\(\Rightarrow\)OF không đổi
Do đó đường thẳng AB luôn đi điểm F cố định

Chọn đáp án A.
Ta có: AC vuông góc BD tại O nên: 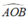 = 90°
= 90°
Suy ra: quỹ tích điểm O là đường tròn đường kính AB
vẽ hình ta thấy
do tg ABCD là hình bình hành nên
\(\overrightarrow{AD}\)=\(\overrightarrow{BC}\)
Mà A,D cố định nên\(\Rightarrow\)\(\overrightarrow{AD}\) là vecto cố định
\(\Rightarrow\)T\(\overrightarrow{AD}\)(B)=C
Mà B thuộc (C) \(\Rightarrow\)C thuộc (C')là ảnh của (C) qua T\(\overrightarrow{AD}\)