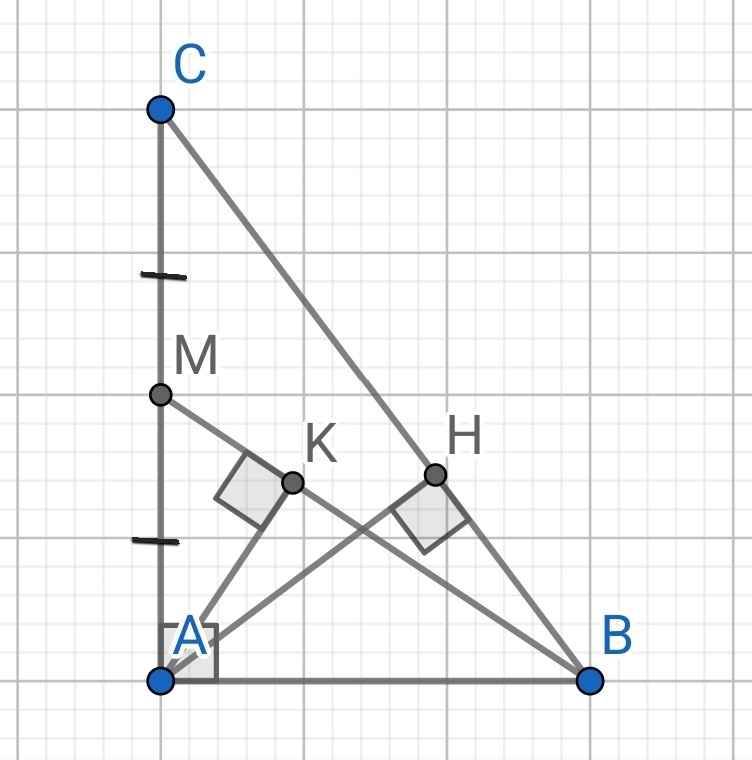
cho tam giác abc có góc abc 45 độ acb= 30 gọi M là trung điểm của AC . Tính số đo của góc AMB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 10 2023
a: BC=BH+CH
=4+6
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{4\cdot6}=2\sqrt{6}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{4\cdot10}=2\sqrt{10}\left(cm\right)\\AC=\sqrt{6\cdot10}=2\sqrt{15}\left(cm\right)\end{matrix}\right.\)
b: M là trung điểm của AC
=>\(AM=\dfrac{AC}{2}=\sqrt{15}\left(cm\right)\)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\sqrt{\dfrac{2}{3}}\)
=>\(\widehat{AMB}\simeq39^0\)
c: ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)
TT
10 tháng 1 2021
Bạn gõ thừa chữ "cân"
a/ Xét t/g ABC vuông tại A có
\(\widehat{ABC}+\widehat{ACB}=90^o\) (t/c)
\(\Rightarrow\widehat{ABC}=90^o-40^o=50^o\)
b/ Xét t/g AMB và t/g EMC có
AM = EM
\(\widehat{AMB}=\widehat{EMC}\) (đối đỉnh)MB = MC
=> t/g AMB = t/g EMC (c.g.c)c/ Có
AE // CK
=> \(\widehat{AEK}+\widehat{EKC}=180^o\) (tcp)
=> \(\widehat{AEK}=\widehat{AEC}+\widehat{CEK}=90^o\)
Xét t/g ABC vuông tại A có AM là đường trung tuyến
=> AM = 1/2 BC = BM
=> t/g AMB cân tại A
=> \(\widehat{ABC}=\widehat{BAM}\)
Mà \(\widehat{BAM}=\widehat{CEA}\)
=> \(\widehat{CBA}+\widehat{CEK}=90^o\)
=> \(\widehat{CEK}=\widehat{ACB}\)
28 tháng 4 2023
a: góc ABC=180-50-70=60 độ
b: Vì góc IBC=1/2*góc ABC
nên BI là phân giác của góc ABC
Vì góc ICB=1/2*góc ACB
nên CI là phân giác của góc ACB
c: Xét ΔBFI vuông tại F và ΔBDI vuông tại D có
BI chung
góc FBI=góc DBI
=>ΔBFI=ΔBDI
=>ID=IF
Xét ΔCDI vuông tại D và ΔCEI vuông tại E co
CI chung
góc DCI=góc ECI
=>ΔCDI=ΔCEI
=>ID=IE=IF
=>I là giao của 3 đường trung trực ΔDEF
KV
3 tháng 6 2023
Do M là trung điểm của BC và \(\Delta ABC\) vuông tại A
\(\Rightarrow AM\) là đường trung tuyến ứng với cạnh huyền BC
\(\Rightarrow AM=BM=CM=\dfrac{BC}{2}\)
\(\Rightarrow\Delta MAB\) cân tại M
\(\Rightarrow\widehat{BAM}=\widehat{ABM}=30^0\)