Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC=BH+CH
=4+6
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{4\cdot6}=2\sqrt{6}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{4\cdot10}=2\sqrt{10}\left(cm\right)\\AC=\sqrt{6\cdot10}=2\sqrt{15}\left(cm\right)\end{matrix}\right.\)
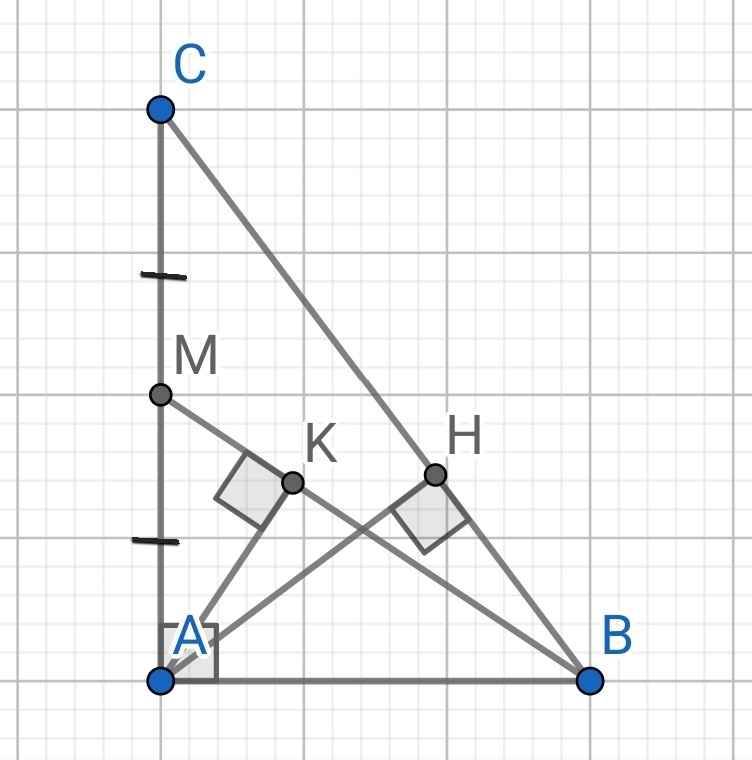
b: M là trung điểm của AC
=>\(AM=\dfrac{AC}{2}=\sqrt{15}\left(cm\right)\)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\sqrt{\dfrac{2}{3}}\)
=>\(\widehat{AMB}\simeq39^0\)
c: ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)

Bài 1
a) \(BC=125\Rightarrow BC^2=15625\)
\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{AB}{3}=\frac{AC}{4}\)từ đây ta có \(\frac{AB^2}{9}=\frac{AC^2}{16}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có
\(\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{25}=\frac{BC^2}{25}=\frac{15625}{25}=625\)
\(\frac{AB^2}{9}=625\Rightarrow AB=75\)
\(\frac{AC^2}{16}=625\Rightarrow AC=100\)
Áp dụng hệ thức lượng trong tam giác vuông ta có
\(AB^2=BH\cdot BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{5625}{125}=45\)
\(AC^2=CH\cdot BC\Rightarrow CH=\frac{AC^2}{BC}=\frac{10000}{125}=80\)
b.c) làm tương tự cũng áp dụng HTL trong tam giác vuông
Bài 2
Hình bạn tự vẽ
Ta có \(EH\\ AC\left(EH\perp AB;AC\perp AB\right)\Rightarrow\frac{BE}{AB}=\frac{BH}{BC}\Rightarrow BE=\frac{AB\cdot BH}{BC}\Rightarrow BE^2=\frac{AB^2\cdot BH^2}{BC^2}\)
\(\Leftrightarrow BE^2=\frac{BH\cdot BC\cdot BH^2}{BC^2}=BH^3\)
Bài 3 Đề bài này không đủ dữ kiện tính S của ABC

Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)

kẻ BK vuongAC ^CBK vuong tai K và ^C = 30 độ = > tam giácCBK nửa đều BK = BC/2 = 5,5 ^KBC = 180-(BKA+^C) = 60độ ^KBA = ^KBC-^ABC = 22 độ = >tam giác KBA có KBA = 22 độ = >AB = BK:sinKBA = 5,5:sin22 = 5,93194 AN = AB.sinABN = 3,65207 b) AC = 2AN = 7,30414
38 38 o o A B C K N
Kẻ \(BK\perp AC\left(K\in AC\right)\)
Trong tam giác vuông BKC có:
\(\widehat{KBC}=60^o-30^o=60^o\)
\(\Rightarrow\widehat{KBA}=60^o-38^o=22^o\)
BC = 11 (cm) => BK = 5,5 (cm) ( tính chất cạnh đối diện góc 30° trong tam giác vuông bằng nửa cạnh huyền )
Xét tam giác ABK vuông tại K : \(\cos KBA=\frac{BK}{AB}\)
\(\Rightarrow AB=\frac{BK}{\cos KBA}=\frac{5,5}{\cos22^o}\approx5,93\left(cm\right)\)
Xét tam giác ANB vuông tại N : \(\sin ABN=\frac{AN}{AB}\)
\(\Rightarrow AN=AB\sin ABN=5,93.\sin38^o\approx3,65\left(cm\right)\)
b) Xét tam giác ANC vuông tại N : \(\sin ACN=\frac{AN}{AC}\)
\(AC=\frac{AN}{\sin ACN}\approx\frac{3,65}{\sin30^o}\approx7,3\left(cm\right)\)

Giúp mình với ạ..