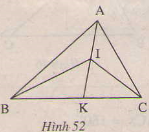
Cho hình 52. Hãy so...
Đọc tiếp
Cho hình 52. Hãy so sánh:
a) và
.
b) và
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
4 tháng 4 2021
Hình thì bạn tự vẽ nhé. Mk k bt vẽ ở trên này :))
a) - Có AB=BE (gt) mà 2 chiều rộng hình chữ nhật thì = nhau -> AB= BE= CD ->BE=CD
- Vì là HCN -> góc ABC=góc DCB= 90 độ
mà góc ABC và góc MBE là 2 góc kề bù => góc ABC= góc MBE= 180/2= 90 độ => góc MBE= DCB= 90 độ
- Xét tam giác BME và tam giác CMD có:
Góc MBE+ BME+ E= 180 độ (tổng 3 góc của 1 tam giác) và góc C+ CMD+D= 180 độ (tổng 3 góc của 1 tam giác)
mà góc MBE=DCB (cmt), BME=CMD (2 góc đối đỉnh) => góc E= MDC
- Xét tam giác BEM và tam giác CDM có:
góc E= góc MDC (cmt)
BE= CD (cmt)
góc MBE= góc DCB (=90 độ, cmt)
=> Tam giác BEM= tam giác CDM (g-c-g)
b) Vì tam giác BEM= tam giác CDM ( cm câu a) => MB= MC (2 cạnh tương ứng)
c) Câu này thì mk k làm đc tại hình như bạn ghi đề bài bị thiếu hay sai ý. Mk đọc k thấy điểm K và H nên bạn tự làm nhé ^ ^
BN
1 tháng 4 2017
a, Diện tích của mặt cầu là: \(S_c=4\pi r^2\)
Diện tích xung quanh của mặt trụ là: \(S_t=2\pi rh=4\pi r^2\)
Vậy Sc = St
b, Thể tích của khối trụ là: \(V_t=\pi r^2h=2\pi r^2\)
Thể tích của khối cầu là: \(V_c=\dfrac{4}{3}\pi r^2\)
Vậy \(V_t=\dfrac{3}{2}V_c\)
KJ
2
30 tháng 11 2021
\(a,A=\left(1+5+5^2\right)+\left(5^3+5^4+5^5\right)+...+\left(5^{57}+5^{58}+5^{59}\right)\\ A=\left(1+5+5^2\right)+5^3\left(1+5+5^2\right)+...+5^{57}\left(1+5+5^2\right)\\ A=\left(1+5+5^2\right)\left(1+5^3+...+5^{57}\right)\\ A=31\left(1+5^3+...+5^{57}\right)⋮31\\ b,5A=5+5^2+5^3+...+5^{60}\\ \Rightarrow5A-A=4A=5^{60}-1\\ \Rightarrow A=\dfrac{5^{60}-1}{4}=\dfrac{5^{60}}{4}-\dfrac{1}{4}< \dfrac{5^{60}}{4}=B\)
NA
30 tháng 11 2021
a. A = 1 + 5 + 52 + 53 + .... + 559
A = ( 1 + 5 + 52) + (53 + 54 + 55) +.....+ (557 + 558 + 559)
A = (1 + 5 + 52) + 53(1 + 5 + 52) + ..... + 557( 1 + 5 + 52)
A = (1 + 5 + 52)( 1 + 53 +......+ 557)
A = 31(1 + 53+.....+ 557)
Vì có một thừa số 31 nên A ⋮ 31
KJ
2
30 tháng 11 2021
a: \(A=\left(1+5+5^2\right)+...+5^{57}\left(1+5+5^2\right)\)
\(=31\left(1+...+5^{57}\right)⋮31\)
AH
Akai Haruma
Giáo viên
30 tháng 11 2021
Lời giải:
a.
$A=1+5+5^2+5^3+...+5^{59}$
$= (1+5+5^2)+(5^3+5^4+5^5)+....+(5^{57}+5^{58}+5^{59})$
$=(1+5+5^2)+5^3(1+5+5^2)+....+5^{57}(1+5+5^2)$
$=31+5^3,31+,,,,,+5^{57}.31$
$=31(1+5^3+...+5^{57})\vdots 31$ (đpcm)
b.
$A=1+5+5^2+...+5^{59}$
$5A=5+5^2+5^3+...+5^{60}$
$\Rightarrow 4A=5A-A=5^{60}-1< 5^{60}$
$\Rightarrow A< \frac{5^{60}}{4}=B$
LH
20 tháng 4 2017
a)Ta có \(\widehat{BIK}\) là góc ngoài của BAI.
Nên \(\widehat{BIK}>\widehat{BAI}\) (1)
b) \(\widehat{CIK}>\widehat{CAI}\)( Góc ngoài của \(\Delta\) CAI)
Từ (1) và (2) ta có:
\(\widehat{BIK}+\widehat{CIK}>\widehat{BAI}+\widehat{CAI}\)
\(\Rightarrow\widehat{BIC}>\widehat{BAC}\)
20 tháng 4 2017
) Ta có ∠BIK là góc ngoài của ∠BAI( hay là góc ngoài ∠BAK)
Các em lưu ý nếu không hiểu: Góc ngoài của tam giác lớn hơn mỗi ngóc trong không kề với nó (ở đây là tam giác ∆ BIA)
Nên ∠BIK > ∠BAK (1)
b) Góc ∠CIK > ∠CAI (2) (Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có: ∠BIK + ∠CIK > ∠BAK + ∠CAI
Mà ∠BIC = ∠BIK + ∠CIK; ∠BAC = ∠BAK + ∠CAI
⇒ ∠BIC > ∠BAC.
CM
17 tháng 11 2017
A = 0 , 25 × 7 + 0 , 25 2 0 , 4 × 5 2 − 2 5 A = 7 4 + 1 16 . 2 5 .25 − 2 5 A = 29 16 . 48 5 A = 87 5 = 17 2 5
B = 2 89 − 3 178 ⋅ 89 17 + 33 34 B = 4 178 − 3 178 . 89 17 + 33 34 B = 1 178 . 89 17 + 33 34 B = 1 34 + 33 34 = 1
Vậy A>B
a)Ta có BIK là góc ngoài của BAI.
Nên BIK > BAI (1)
hay BIK>BAK
b) CIKCAI > ( Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có:
BIK +CIK >BAI +CAI
=> BIC>BAC