
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


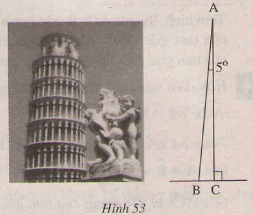
Ta có tam giác vông ABC vuông ở C. Nên +
= 900
Hay 50+ = 900 => 900 - 50 = 850
Mình cũng ko chắc lắm, nhưng theo kiến thức của mình là vậy.
Trong tam giác ABC ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180\)
\(\Rightarrow\widehat{B}=180^0-\left(\widehat{A}+\widehat{C}\right)=180^0-\left(5^0+90^0\right)=85^0\)
Vậy góc B = 85 độ

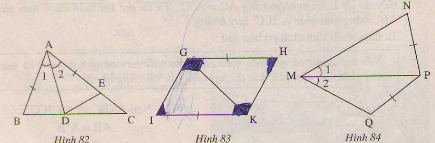
h82:
trong tam giac adb va tam giac ade co
ad:canh chung
A1=a2
ab=ae(gia thiet)
do do tam giac adb = tam giac ade(c.g.c)
h83:
trong tam giac hgk va tam giac ikg co
gk:canh chung
goc hgk =goc ikg
gk=ik(gia thiet)
do do tam giac hkg = tam giac ikg(c.g.c)
h84:
trong tam giac pnm va tam giac pqm co:
mp:canh chung
goc m1=goc m2
pn=pq(gia thiet)
nhung vi goc m1 va goc m2 khong phai goc xen giua
do do tam giac pmn khong bang tam giac pqm

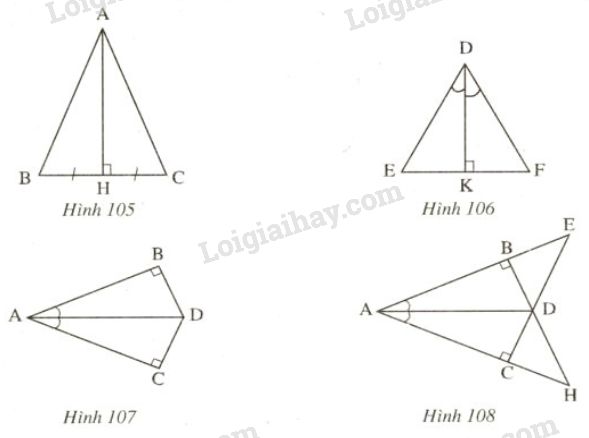
Tam giác DKE có:
+
+
=900 (tổng ba góc trong của tam giác).
+800 +400=1800
=1800 -1200=
Nên
∆ ABC và ∆KDE có:
AB=KD(gt)
=
=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .
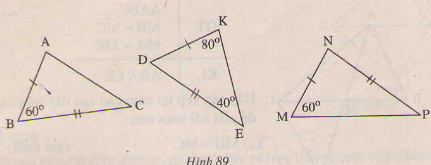
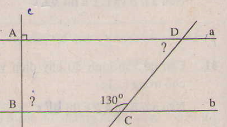
- Tam giác DKE có: ∠D + ∠K + ∠E = 1800 (tổng ba góc trong của tam giác).
hay ∠D + +800 +400 = 1800
⇒∠D = 1800 -1200 = 600
Xét ∆ ABC và ∆KDE có:
AB = KD(gt)
∠B = ∠D ( cùng = 600 )
và BE = ED (gt)
Do đó ∆ABC= ∆KDE (c.g.c)
- Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .

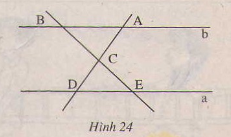
góc CAB = góc CDE
góc CBA = góc CED
góc ACB = góc DCE
chúc bạn học tốt![]()

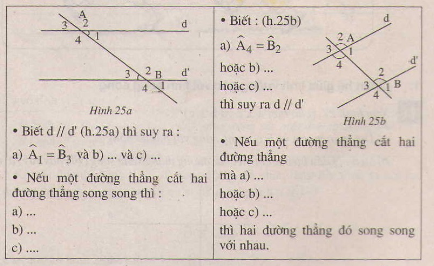
- Hình 25a
Biết d // d' (h.25a) thì suy ra:
a) A1=B3 và b) A1=B1 và c) A1+B2=180độ
Nếu một đường thẳng cắt hai đường thẳng song song thì:
a) Hai góc so le trong bằng nhau
b) HAi góc đồng vị bằng nhau
c) Hai góc trong cùng phía bù nhau
- Hình 25b
Biết
a) A4=B2
hoặc b) A2=B2
hoặc c) A4+B3=180 độ
thì suy ra d//d'
Nếu một đường thẳng cắt hai đường thẳng mà
a) Hai góc so le trong bằng nhau
hoặc b) Hai góc đồng vị bằng nhau
hoặc c) hai góc trong cùng phía bù nhau
thì hai đường thằng đó song song vs nhau.
- Biết d // d' thì suy ra:
a) A1 = B3 và b) A4 = B2 và c) A2 = B2
- Nếu 1 đường thẳng cắt 2 đường thẳng song song thì:
a) 2 góc so le trong = nhau
b) 2 góc đồng vị = nhau
c) 2 góc trong cùng phía bù nhau
- Nếu 1 đường thẳng cắt 2 đường thẳng
mà a) 2 góc so le trong = nhau
hoặc b) 2 góc đồng vị = nhau
hoặc c) 2 góc trong cùng phía bù nhau
thì 2 đường thẳng đó song song với nhau.

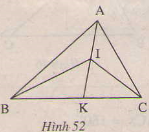
a)Ta có BIK là góc ngoài của BAI.
Nên BIK > BAI (1)
hay BIK>BAK
b) CIKCAI > ( Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có:
BIK +CIK >BAI +CAI
=> BIC>BAC