Chứng minh rằng: a2 + b2 -2ab +1 > 0 với mọi số a,b
Cảm ơn trước ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
Các cao nhân giúp em ạ
9 tháng 6 2021
1) 52005 +52003 = 52003(52+1)=52003(25+1) = 52003.26
Mà 26 chia hết cho 13 => ...
2)a2 + b2 + 1 ≥ ab + a + b <=> 2a2+2b2+2 ≥ 2ab + 2a +2b (*nhân cả hai vế với 2*)
<=> 2a2-2ab+2b2 +2 -2a -2b ≥0 (*chuyển vế phải sang vế trái và đổi dấu*)
<=> (a2-2ab+b2)+(a2-2a+1)+(b2-2b+1)≥0
<=> (a-b)2+(a-1)2+(b-1)2≥0
=> Bất đẳng thức đúng
=> đpcm
3) Ta có a+b+c=0
<=> a+b = -c
<=> (a+b)3=(-c)3
<=> a3+3a2b+3ab2+b3= -c3
<=> a3+b3+c3= -3a2b -3ab2 (*chuyển vế*)
<=> a3+b3+c3= -3ab(a+b) = -3ab(-c)=3abc (*do a+b = -c*)
PT
1
H
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2023
BĐT cần chứng minh tương đương:
\(a^2+b^2+c^2\ge2ab-2bc+2ca\)
\(\Leftrightarrow a^2+b^2+c^2+2bc-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow a^2+\left(b+c\right)^2-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow\left(a-b-c\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
CM
24 tháng 1 2019
a) Biến đổi vế trái:
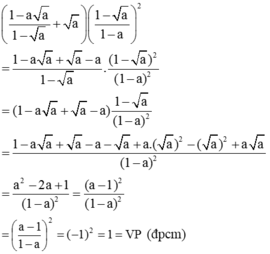
b) Biến đổi vế trái:
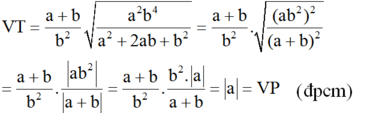
( v ì a + b > 0 n ê n | a + b | = a + b ; b 2 > 0 )
9 tháng 12 2021
Vì a,b,c là 3 cạnh tam giác nên \(a+b>c\Leftrightarrow ac+bc>c^2\)
CMTT: \(ab+bc>b^2;ab+ac>a^2\)
Cộng vế theo vế \(\Leftrightarrow a^2+b^2+c^2< ab+bc+ca+ab+bc+ca\)
\(\Leftrightarrow a^2+b^2+c^2< 2ab+2bc+2ca\\ \Leftrightarrow a^2+b^2+c^2-2ab-2bc-2ca< 0\)
KH
20 tháng 4 2020
\(1.CMR:\left(a+b\right)\left(\frac{1}{a}+\frac{1}{b}\right)\ge4\)
\(\left(a+b\right)\left(\frac{1}{a}+\frac{1}{b}\right)=1+\frac{b}{a}+\frac{a}{b}+1=\frac{a}{b}+\frac{b}{a}+2\)
Áp dụng BĐT AM-GM ta có:
\(\frac{a}{b}+\frac{b}{a}\ge2\sqrt{\frac{a}{b}.\frac{b}{a}}=2\)
\(\Rightarrow\frac{a}{b}+\frac{b}{a}+2\ge2+2=4\)
Dấu '' = '' xảy ra khi \(a=b\)
\(2.\\ a.CMR:a^2+2b^2+c^2-2ab-2bc\ge0\forall a,b,c\)
\(a^2+2b^2+c^2-2ab-2bc=a^2-2ab+b^2+c^2-2bc+b^2=\left(a-b\right)^2+\left(b-c\right)^2\ge0\forall a,b,c\)
Dấu '' = '' xảy ra khi \(a=b=c\)
\(b.CMR:a^2+b^2-4a+6b+13\ge0\forall a,b\)
\(a^2+b^2-4a+6b+13=\left(a^2-4a+4\right)+\left(b^2+6b+9\right)=\left(a-2\right)^2+\left(b+9\right)^2\ge0\forall a,b\)
Dấu '' = '' xảy ra khi \(\left\{{}\begin{matrix}a=2\\b=-9\end{matrix}\right.\)
Ta có : a2 + b2 - 2ab + 1
= a2 - 2ab + b2 + 1
= (a - b)2 + 1
mà (a - b)2 > 0 \(\forall\) a,b
=> (a - b)2 + 1 > 0
Vậy a2 + b2 - 2ab + 1 > 0