Tại sao:
\(^{x^0=1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
23 tháng 8 2021
Đơn giản là em đang xem một lời giải sai. Việc khẳng định $P\leq 0$ hoặc $P>0$ rồi kết luận hàm số không có GTLN là sai.
Bởi vậy những câu hỏi ở dưới là vô nghĩa.
Việc gọi $P$ là hàm số lên lớp cao hơn em sẽ được học, còn bây giờ chỉ cần gọi đơn giản là phân thức/ biểu thức.
Hàm số, có dạng $y=f(x)$ biểu diễn mối liên hệ giữa biến $x$ với biến phụ thuộc $y$. Mỗi giá trị của $x$ ta luôn xác định được một giá trị tương ứng của $y$.
AH
Akai Haruma
Giáo viên
23 tháng 8 2021
$P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}=1+\frac{1}{\sqrt{x}-1}$
Để $P_{\max}$ thì $\frac{1}{\sqrt{x}-1}$ max
Điều này xảy ra khi $\sqrt{x}-1$ min và có giá trị dương
$\Leftrightarrow x>1$ và $x$ nhỏ nhất
Trong tập số thực thì em không thể tìm được số lớn hơn 1 mà nhỏ nhất được. Như kiểu $1,00000000000000000000....$ (vô hạn đến không biết khi nào thì kết thúc)
Do đó $P$ không có max
Min cũng tương tự, $P$ không có min.
22 tháng 4 2022
ờ thì do 2x^2 =2x.2x- 1x cho nên có thừa số chung là x nên như v
22 tháng 4 2022
có j thì bn kết bn với mình mình chỉ cho tk : ntd11223344
22 tháng 7 2023
`a, x = 0 <=> (0^2-1)/(2.0+1) = -1/1 = -1`
`b,` Biểu thức không xác định vì mẫu `= 0`
PQ
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 7 2021
Nhìn đồ thị ta thấy \(f\left(x\right)\) tiếp xúc trục hoành tại điểm \(x=1\) nên \(x=1\) là nghiệm kép (đồ thị cắt trục hoành tại điểm nào thì đó là nghiệm đơn, tiếp xúc là nghiệm kép)
23 tháng 4 2016
Ta có \(f'\left(x\right)=3ax^2+2bx+c;f"\left(x\right)=6ax+2b\)
Hàm số \(f\left(x\right)\) đạt cực tiểu tại \(x=0\) khi và chỉ khi
\(\begin{cases}f'\left(0\right)=0\\f"\left(0\right)>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\2b>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\b>0\end{cases}\left(1\right)\)
Hàm số \(f\left(x\right)\) đạt cực đại tại \(x=1\) khi và chỉ khi \(\begin{cases}f'\left(1\right)=0\\f"\left(1\right)< 0\end{cases}\)\(\Leftrightarrow\begin{cases}3a+2b+c=0\\6a+2b< 0\end{cases}\)
\(\begin{cases}f\left(0\right)=0\\f\left(1\right)=1\end{cases}\)\(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) \(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) (3)
Từ (1), (2), (3) suy ra \(a=-2;b=3;c=0;d=0\)
Kiểm tra lại \(f\left(x\right)=-2x^3+3x^2\)
Ta có \(f'\left(x\right)=-6x^2+6x;f"\left(x\right)=-12x+6\)
\(f"\left(0\right)=6>0\), hàm số đạt cực tiểu tại \(x=0\)
\(f"\left(1\right)=-6< 0\), hàm số đạt cực đại tại \(x=1\)
Vậy \(a=-2;b=3;c=0;d=0\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2022
3 là mệnh đề đúng, do khi \(\Delta< 0\) thì \(a.f\left(x\right)>0\) ; \(\forall a\ne0\)
NT
1
18 tháng 5 2018
Vì k\(\in\)N* nên k nhỏ nhất khi k=1
Xét k nhỏ nhất khi k=1
\(\Rightarrow\)2*1+1:2=1.5>0
Vì k\(\in\)N* mà k là số có 1 chữ số
\(\Rightarrow\)k lớn nhất khi k=9
Xét k=9
\(\Rightarrow\)2*9+1:2=9.5<10
Người ta quy ước bất cứ số nào có muc bằng 0 thì số đó bằng 1
với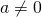
mà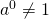 
thì sẽ có mâu thuẫn
Thật vậy, giả sử rằng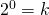
và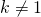 
(*) khi đó một bài toán hết sức đơn giản sau đây sẽ có hai đáp số:
Tính giá trị của biểu thức
Là một bài toán hết sức đơn giản, đến mức quá tầm thường phải không, nhưng ta lại có thể giải nó theo 2 cách khác nhau với những đáp số khác nhau.
CÁCH 1: THỰC HIỆN PHÉP CHIA
Thực hiện một phép chia mà ai ai cũng biết. Thật là hiển nhiên, một số chia cho chính nó thì bằng 1 chứ còn bằng mấy? Vậy
Nhưng mặt khác:
CÁCH 2: ÁP DỤNG TÍNH CHẤT LŨY THỪA
Áp dụng tính chất của lũy thừa, ta có:
Theo giả sử ở trên thì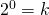
nên
Từ (1)(2) ta có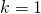
, mẫu thuẫn với giả thiết (*): 
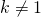!! Sở dĩ có mâu thuẫn như thế là do ta đã giả sử 
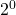khác 1.
Như vậy, vớ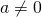i
thì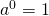 
và có thể nói định nghĩa này nhằm để hợp lý hóa hay có nguồn gốc từ phép toán 
.
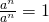Đó nha
kb nhé
CHÚC BẠN HỌC TỐT!