
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Căn x >-1 thì có tìm được x không ạ. Nếu được giải ra giúp mình nhá còn không thì chỉ là tại sao nhá

\(\sqrt{x}>-1=>\sqrt{x}+1>0\)(1)
ta thấy \(\sqrt{x}\ge0=>\sqrt{x}+1\ge1\left(2\right)\)
(1)(2)=>vô lí nên ko tìm đc x

Đơn giản là em đang xem một lời giải sai. Việc khẳng định $P\leq 0$ hoặc $P>0$ rồi kết luận hàm số không có GTLN là sai.
Bởi vậy những câu hỏi ở dưới là vô nghĩa.
Việc gọi $P$ là hàm số lên lớp cao hơn em sẽ được học, còn bây giờ chỉ cần gọi đơn giản là phân thức/ biểu thức.
Hàm số, có dạng $y=f(x)$ biểu diễn mối liên hệ giữa biến $x$ với biến phụ thuộc $y$. Mỗi giá trị của $x$ ta luôn xác định được một giá trị tương ứng của $y$.
$P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}=1+\frac{1}{\sqrt{x}-1}$
Để $P_{\max}$ thì $\frac{1}{\sqrt{x}-1}$ max
Điều này xảy ra khi $\sqrt{x}-1$ min và có giá trị dương
$\Leftrightarrow x>1$ và $x$ nhỏ nhất
Trong tập số thực thì em không thể tìm được số lớn hơn 1 mà nhỏ nhất được. Như kiểu $1,00000000000000000000....$ (vô hạn đến không biết khi nào thì kết thúc)
Do đó $P$ không có max
Min cũng tương tự, $P$ không có min.

Bài 1:
Nếu chị nhớ không nhầm thì phải là \(\left[\begin{matrix} \frac{1}{2}\leq x< 2\\ 0< x<\frac{1}{2}\end{matrix}\right.\)
Tức là $x$ nhận các khoảng giá trị sau:
\(0< x< \frac{1}{2}\); \(x=\frac{1}{2}\); \(\frac{1}{2}< x< 2\)
Vậy có nghĩa $0< x< 2$ (rất dễ hiểu mà????)
Bài 2:
Ngoặc nhọn dùng khi muốn biểu thị hai/ nhiều phương trình/ bất phương trình đồng thời xảy ra cùng một lúc
Ngoặc vuông dùng khi muốn biểu thị cái này hoặc cái kia xảy ra.
Bài trên phải dùng ngoặc vuông là sao em? Ngoặc nhọn thường xuất hiện trong bài toán giải hệ phương trình, bất phương trình. Còn ngoặc vuông thì thường dùng kết luận nghiệm của pt/ bpt.
Kết hợp điều kiện thì dùng ngoặc nhọn. Ví dụ $\sqrt{x+1}+\sqrt{2-x}$ thì việc $x+1\geq 0$ và $2-x\geq 0$ phải đồng thời xảy ra cùng lúc.

Bạn chỉ cần hiểu là căn bậc hai số học của là một số x sao cho \(x^2=a\) và \(x\ge0\) thôi

Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.

Δ'=(m+1)2-1(m-4)
=m2+2m+1-m+4
=m2+m+5>0
=(m+1/2)+19/4>0 với mọi m
=> PT luôn có 2 nghiệm phân biệt
Theo hệ thức vi-ét ta có:
x1+x2=2m+2
x1.x2=m-4
mà /x1-x2/
=>(x1+x2)-4.x1x2
lắp ghép vào và tự tính ra nhé bạn!!!
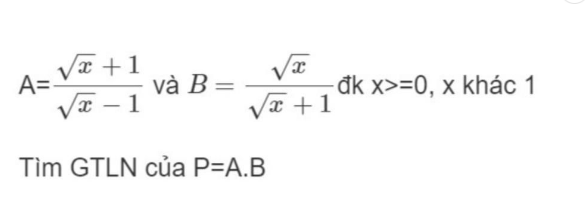

Ta thấy : `(x-1)^2>=0 , ∀x`
`=>(x-1)^2-1>=-1 , ∀x`
`->(x-1)^2-1` chưa chắc lớn hơn `0` vì giá trị nhỏ nhất của nó bằng `-1` khi `x=1`