cho ΔABC, biết AB = 6cm, góc B= 420. Đường cao AK chia đoạn BC thành 2 đoạn thẳng BK và CK = 6cm. Tính BK,AK,AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
15 tháng 5 2021
a/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
BK là pg \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AK}{CK}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
=> \(\dfrac{AK}{3}=\dfrac{CK}{5}=\dfrac{AC}{8}=1\)
=> AK = 3cm ; CK = 5 cm
b/ Xét t/g ABC và t/g HBA có
\(\widehat{ABC}\) chung
\(\widehat{BAC}=\widehat{AHB}=90^o\)
=> t/g ABC ~ t/g HBA
=> \(\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
=> \(AB^2=BC.HB\)
c/ \(\dfrac{BC}{AC}=\dfrac{10}{6}=\dfrac{5}{3}\)
t/g ABC ~ t/g HBA vs tỉ số đồng dạng là 5/3
10 tháng 4 2023
a, Xét tam giác CKA và tam giác CAB có
góc C chung
góc BAC= góc AKC (=90 độ)
=> tam giác CKA đồng dạng với tam giác CAB
b, vì tam giác CKA đồng dạng với tam giác CAB
=>CA/BC=CK/CA
=>CA^2=BC.CK( ĐPCM)
c,
áp dụng định lý py-ta-go vào tam giác ABC vuông tại A
BA^2+AC^2=BC^2
=>36+64=BC^2
=>BC=10 cm
Xét tam giác ABC
AB/AE=BC/CE
=>6/AE=10/8-AE
<=>6(8-AE)=10AE
<=>48-6AE-10AE=0
<=>-16AE=-48
<=>AE=3
=>AC-AE=CE
<=>8-3=CE
<=>CE=5
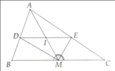
trong ΔAKB vuông tại K,
ta có: cgv = ch. cos(kề)
hay: BK = AB . cos B
BK = 6 . cos 42 0 ∼4,4 cm
lại có: cgv = ch . sin (đối)
AK = AB . sin B
AK = 6 . sin 420 ∼4cm
Áp dụng định lí Py - ta - go vào ΔAKC vuông tại K, ta có:
AC2 = AK2 + CK2
hay AC2 = 42 + 62 = 52
=> AC = \(\sqrt{52}\) ∼ 7,2 cm