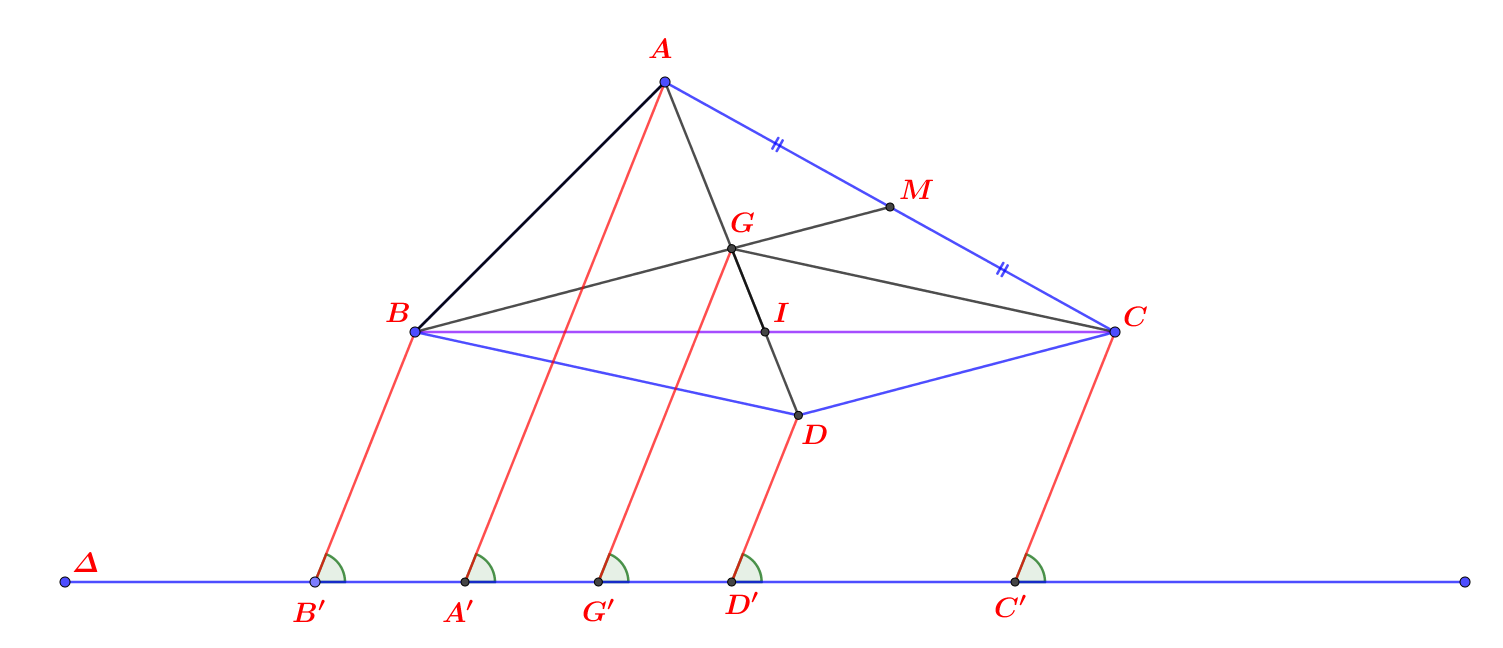
Xin phép được nhờ quý thầy cô giáo và các bạn giúp đỡ em bài toán nâng cao lớp 8 học kỳ 1.
#đường_trung_bình_của_tam_giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 3 2022
\(\Leftrightarrow\dfrac{2bc}{2bc+a^2}+\dfrac{2ac}{2ac+b^2}+\dfrac{2ab}{2ab+c^2}\le2\)
\(\Leftrightarrow\dfrac{2bc}{2bc+a^2}-1+\dfrac{2ac}{2ac+b^2}-1+\dfrac{2ab}{2ab+c^2}-1\le2-3\)
\(\Leftrightarrow\dfrac{a^2}{2bc+a^2}+\dfrac{b^2}{2ac+b^2}+\dfrac{c^2}{2ab+c^2}\ge1\)
BĐT trên đúng theo C-S:
\(\dfrac{a^2}{2bc+a^2}+\dfrac{b^2}{2ac+b^2}+\dfrac{c^2}{2ab+c^2}\ge\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2+2ab+2bc+2ca}=1\)
Dấu "=" xảy ra khi \(a=b=c\)
XO
5 tháng 4 2022
Với p = 2 => 8p2 +1 = 33 (loại)
Với p = 3 => 8p2 + 1 = 73 (tm)
Với p > 3 => Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Với p = 3k + 1 => 8p2 + 1 = 8(3k + 1)2 + 1
= 72k2 + 48k + 9 = 3(24k2 + 16k + 3) \(⋮3\)(loại)
Với p = 3k + 2 => 8p2 + 1 = 8(3k + 2)2 + 1
= 72k2 + 96k + 33 = 3(24k2 + 32k + 11) \(⋮3\)(loại)
Vậy p = 3 thì 8p2 + 1 \(\in P\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
- Với \(p=2\) ko thỏa mãn
- Với \(p=3\Rightarrow8p^2+1=73\) là số nguyên tố (thỏa mãn)
- Với \(p>3\Rightarrow p^2\equiv1\left(mod3\right)\)
\(\Rightarrow p^2=3k+1\)
\(\Rightarrow8p^2+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)\) là số lớn hơn 3 và chia hết cho 3
\(\Rightarrow8p^2+1\) là hợp số (ktm)
Vậy \(p=3\) là SNT duy nhất thỏa mãn yêu cầu
XO
5 tháng 4 2022
Với p = 2 => 2p + p2 = 8 (loại)
Với p = 3 => 23 + 32 = 17 (loại)
Nhận thấy với p > 3 => p lẻ
Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Khi đó P = 2p + p2
= (2p + 1) + (p2 - 1)
Vì p lẻ => 2p + 1 = (2 + 1).(2p - 1 - 2p - 2 + ... + 1) \(⋮3\)(1)
Với p = 3k + 1 => p2 - 1 = (p - 1)(p + 1) = (3k + 1 - 1)(3k + 1 + 1)
= 3k(3k + 2) \(⋮3\) (2)
Từ (1) ; (2) => P \(⋮3\)(loại)
Với p = 3k + 2 => p2 - 1 = (p - 1)(p + 1) = (3k + 2 - 1)(3k + 2 + 1)
= 3(k + 1)(3k + 1) \(⋮\)3 (3)
Từ (1) ; (3) => P \(⋮3\)
=> p = 3 là giá trị cần tìm
5 tháng 4 2022
Dạ hay quá, em cám ơn thầy ạ
Em gặp mấy bài toán về chủ đề : Đồng Dư Thức- khó quá
May được thầy giúp đỡ ạ!
19 tháng 4 2022
Xét p=2\(\Rightarrow p^4+29=45=3^2.5\), có 6 ước số là SND, loại
Xét p=3\(\Rightarrow p^4+29=110=2.5.11\), có 8 ước số là SND, tm
Xét p=5\(\Rightarrow p^4+29=654=2.3.109\) , có 8 ước số là SND, tm
Xét p\(\ge6\). Do p là SNT nên p có dạng \(6k+1\) hoặc \(6k-1\) (k\(\in N\)*)
TH1: p=6k+1
Khi đó ta có \(p^4+29=\left(6k+1\right)^4+29\equiv1+29\equiv0\left(mod6\right)\)
Ta cũng có: \(p^4+29=\left(6k+1\right)^4+29\equiv0\left(mod5\right)\)
vì \(\left(6k+1\right)⋮5̸\)
\(\Rightarrow p^4+29=6.5.a=2.3.5.a\)(a là STN)\(\Rightarrow p^4+29\) có nhiều hơn 8 ước số nguyên dương, loại.
TH2: p=6k-1. Chứng minh tương tự ta thấy không có p thoả mãn
\(\Rightarrow p\ge6\) không thoả mãn
Vậy....
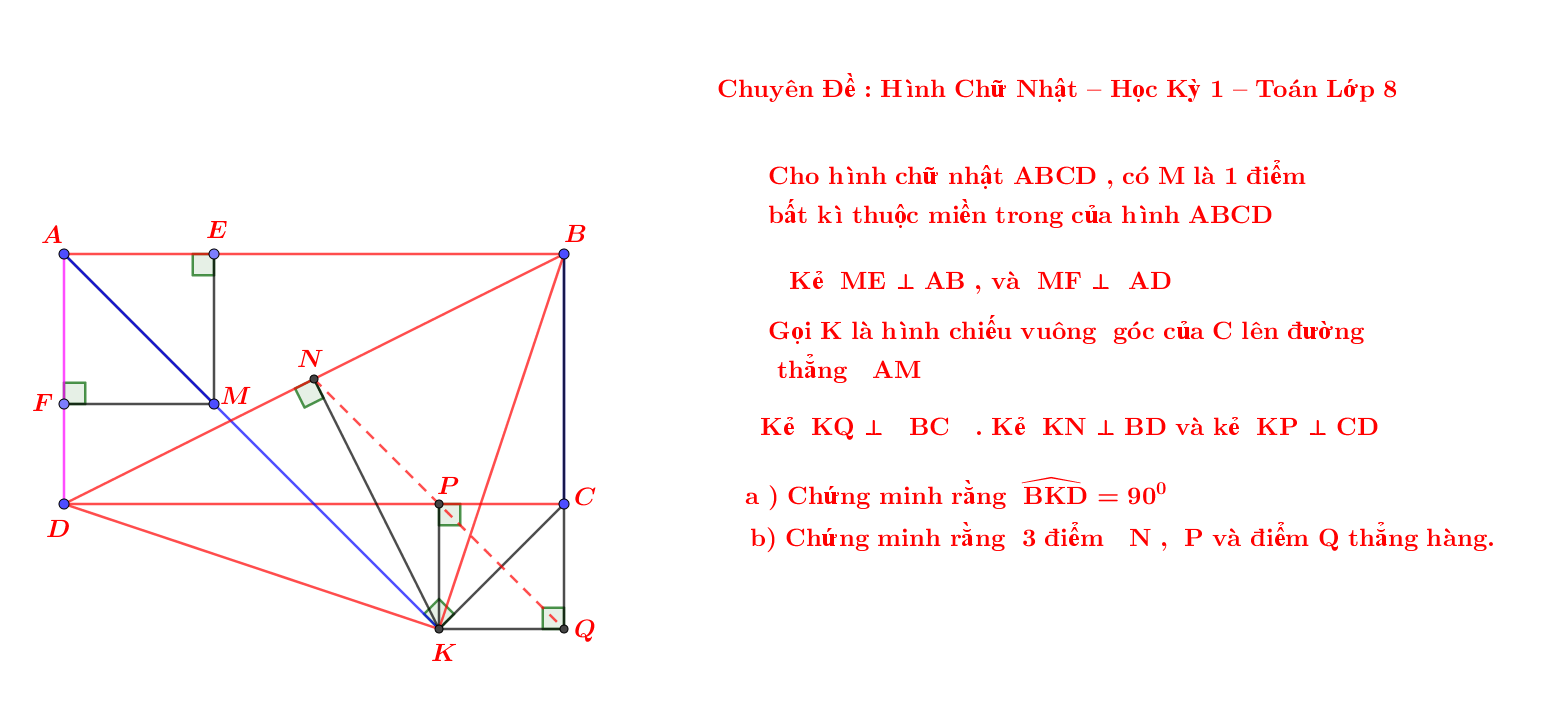
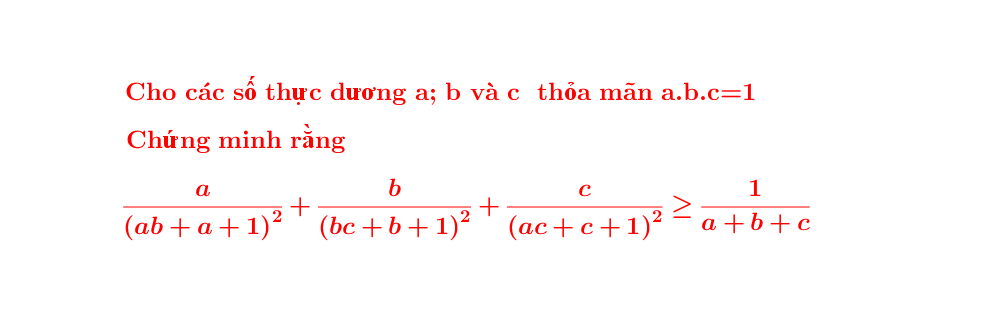
Hình vẽ minh họa cho bài toán