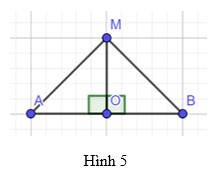
cho M la điểm tùy ý trên đường trung trực của đoạn thẳng AB chứng tam giác MAB là tam giác cân.Hãy rút ra một nhận xét tổng quát về điểm thuộc đường trung trực của một đoạn thẳng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Theo giả thiết ta có O là trung điểm AB \( \Rightarrow \) AO = OB
Xét tam giác AOM và tam giác BOM có :
OM là cạnh chung
AO = OB
\(\widehat {MOA} = \widehat {MOB} = {90^o}\)(do d là trung trực AB)
(c-g-c)
\( \Rightarrow MA = MB\) (cạnh tương ứng)
7 tháng 11 2021
a: Ta có:M nằm trên đường trung trực của AB
nên MA=MB
IM
1
5 tháng 7 2021
Vì 2 điểm A,B nằm trên đường trung trực của đoạn thẳng MN nên A,B cách đều hai đầu mút
Xét tam giác MAB và tam giác NAB ta có :
MA = NA
MB = NB
Cạnh MN chung
Do đó tam giác MAB bằng tam giác NAB (c.c.c)
KN
10 tháng 10 2020
Gọi I là giao điểm của đường trung trực đoạn HC và tia phân giác ^BHC => I là điểm cố định
I nằm trên đường trung trực của HC nên IH = IC => ∆IHC cân tại I => ^IHC = ^ICH
Lại có: ^IHC = ^IHM (Do HI là tia phân giác của ^BHC, theo cách chọn điểm phụ) => ^IHM = ^ICH hay ^IHM = ^ICN
Xét ∆ICN và ∆IHM có:
IC = IH (theo cách chọn hình phụ)
^ICN = ^IHM (cmt)
CN = HM (gt)
Do đó ∆ICN = ∆IHM (c.g.c)
=> IN = IM (hai cạnh tương ứng)
Do đó I thuộc đường trung trực của MN
Vậy đường trung trực của MN luôn đi qua một điểm cố định I (đpcm)
TRẢ LỜI GIÚP MÌNH VỚI MINH ĐANG RẤT GẤP CÓ AI HỌC THẦY CẢNH KO LỚP 7 SÁCH HỌC TỐT TÙ BÀI 96 ĐẾN BAIF113 HÌNH