ab = bc x3 +13
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 12 2021
Câu 4:
\(=\dfrac{a\left(a-b\right)-c\left(a-b\right)}{a\left(a+b\right)-c\left(a+b\right)}=\dfrac{a-b}{a+b}\)
30 tháng 10 2021
\(A=\left(-\dfrac{5}{9}\right).\dfrac{3}{11}+\left(-\dfrac{13}{18}\right).\dfrac{3}{11}=\dfrac{3}{11}\left(-\dfrac{5}{9}-\dfrac{13}{18}\right)\)
\(=\dfrac{3}{11}.\dfrac{-23}{18}=-\dfrac{23}{66}\)
17 tháng 6 2021
Bài 3:
\(\left(x-8\right)\left(x3+8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-8=0\\x3+8=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=\dfrac{-8}{3}\end{matrix}\right.\)
\(\left(4x-3\right)-\left(x+5\right)=3\left(10-x\right)\)
\(4x-3-x-5=30-3x\)
\(4x-x+3x=30+3+5\)
\(6x=38\)
\(x=38:6\)
\(x=\dfrac{19}{3}\)
NT
1
D
4 tháng 8 2021
a/ Chứng minh:
\(\left(x+a\right)\left(x+b\right)\)
\(=x^2+bx+ax+ab\)
\(=x^2+\left(ax+bx\right)+ab\)
\(=x^2+x\left(a+b\right)+ab=VP\) (đpcm)
b/ Chứng minh:
\(\left(x+a\right)\left(x+b\right)\left(x+c\right)\)
\(=\left(x^2+ax+bx+ab\right)\left(x+c\right)\)
\(=x^3+cx^2+ax^2+acx+bx^2+bcx+abx+abc\)
\(=x^3+\left(ax^2+bx^2+cx^2\right)+\left(abx+bcx+acx\right)+abc\)
\(=x^3+x^2\left(a+b+c\right)+x\left(ab+bc+ac\right)+abc=VP\) (đpcm)
CM
7 tháng 5 2018
a) x = 4
b) x = 3
c) x = 2
d) x = 1
e) x = 3
f) x = 2
g) x = 4
h) x = 3
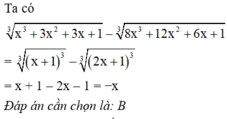
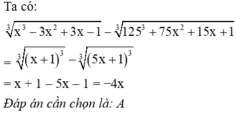
Có ab = ba . 3 + 13
\(\Rightarrow\) 10a + b = ( 10b + a ) . 3 + 13
\(\Rightarrow\) 10a + b = 30b + 3a + 13
\(\Rightarrow\) 7a = 29b + 13 ( bớt cả 2 vế cho 3a và b )
Vì a là số có 1 chữ số nên a < 10 \(\Rightarrow\) 7a < 70 \(\Rightarrow\) 29b + 13 < 70 \(\Rightarrow\) 29b < 57 \(\Rightarrow\) b < 2
\(\Rightarrow\) b = 0 hoặc b = 1
Với b = 0 thì 7a = 13 \(\Rightarrow\) a = \(\frac{13}{7}\) ( vô lý - loại )
Với b = 1 thì 7a = 42 \(\Rightarrow\) a = 6 ( thỏa mãn )
Vậy số tự nhiên cần tìm là 61