nhớ lại trong các kiến thức đã học ( có thể xem lại phần 1.b ) ở trên ) xem tính chất nào có thể phát biểu thành định lí . chỉ dõ giả thuyết và kết luận , với mỗi ddingj lí được phát biểu .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính chất có thể phát biểu thành định lí:
Nếu một đường thẳng cắt hai đường thẳng và trong số các hóc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.
Giả thuyết:
một đường thẳng cắt hai đường thẳng và trong số các góc tạo thành có một cặp góc so le trong bằng nhau.
Kết luận:
hai đường thẳng đó song song với nhau.

Nếu hai đường thằng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.

Hoặc: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó sẽ vuông góc với đường thẳng còn lại .
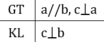

Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
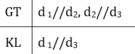

Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
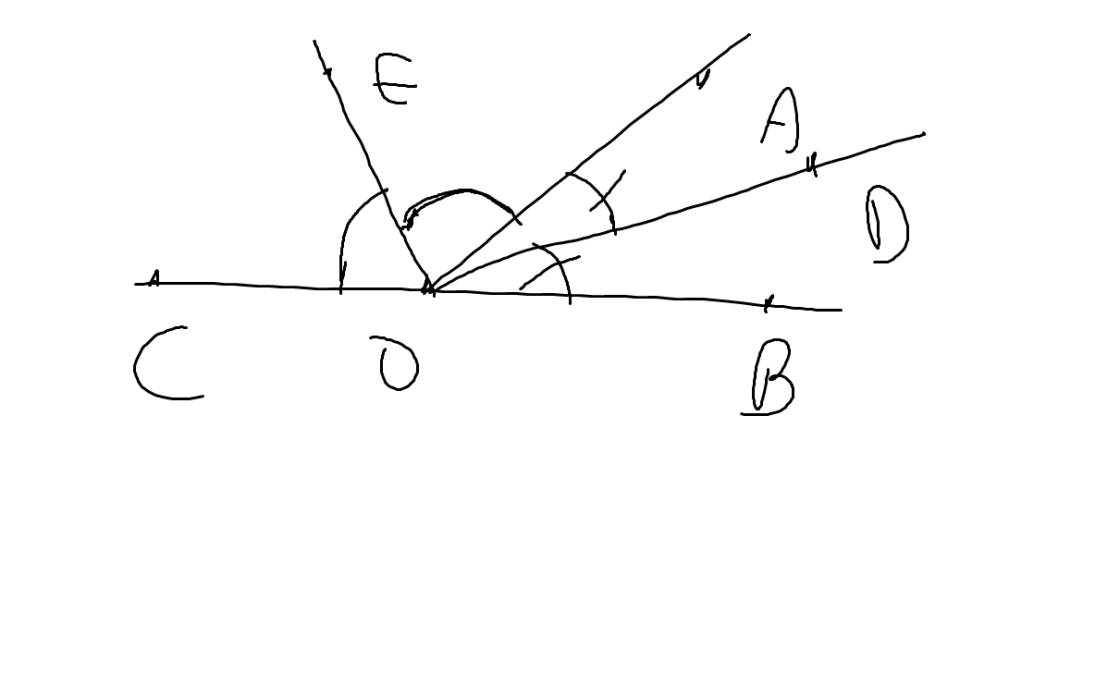
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)

Tham khảo:
a)
Mệnh đề P có dạng \(R \Rightarrow T\)với R: “Hai tam giác bằng nhau” và T: “Diện tích của hai tam giác bằng nhau”
Giả thiết là mệnh đề R: “Hai tam giác bằng nhau”
Kết luận là mệnh đề T: “Diện tích của hai tam giác bằng nhau”
Mệnh đề Q có dạng \(A \Rightarrow B\)với A: “\(a < b\)” và B: “\(a + c < b + c\)”
Giả thiết là mệnh đề A: “\(a < b\)”
Kết luận là mệnh đề B: “\(a + c < b + c\)”
b)
+) Mệnh đề P có thể phát biểu lại như sau:
Hai tam giác bằng nhau là điều kiện đủ để có diện tích của chúng bằng nhau.
Diện tích của hai tam giác bằng nhau là điều kiện cần để hai tam giác bằng nhau.
+) Mệnh đề Q có thể phát biểu lại như sau:
\(a < b\) là điều kiện đủ để có \(a + c < b + c\).
\(a + c < b + c\)là điều kiện cần để có \(a < b\).
c)
Mệnh đề đảo của mệnh đề P có dạng \(T \Rightarrow R\), phát biểu là: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau”.
Mệnh đề này sai nên không là định lí.
Chẳng hạn: Tam giác ABC và tam giác DEF, có diện tích bằng nhau nhưng hai tam giác không bằng nhau.
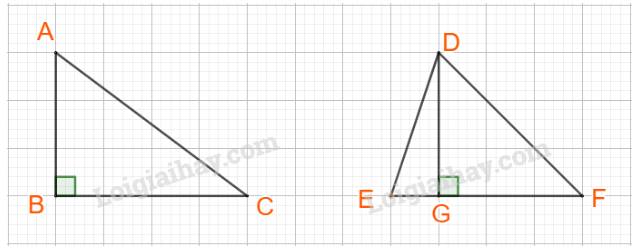
Mệnh đề đảo của mệnh đề Q có dạng \(B \Rightarrow A\), phát biểu là: “Nếu \(a + c < b + c\)thì \(a < b\)”.
Mệnh đề này đúng nên nó cũng là định lí.

Đáp án B
Chỉ có phát biểu số III đúng.
I sai. Vì các cây cùng màu hoa giao phấn với nhau thì đấy là giao phấn không ngẫu nhiễn. Giao phấn không ngẫu nhiên chỉ làm thay đổi thành phần kiểu gen, không làm thay đổi tần số alen của quần thể.
II sai. Vì nếu hạt phần của cây hoa đỏ không có khả năng thụ tinh thì chọn lọc tự nhiên đang chống lại alen A. Do đó sẽ làm giảm tần số alen A, tần số alen a sẽ tăng dần qua các thế hệ.
III đúng. Vì khi tần số alen và thành phần kiểu gen thay đổi một cách đột ngột thì có thể do tác động của các yếu tố ngẫu nhiên.
IV sai. Vì nếu chọn lọc chống lại hoa vàng (Aa) thì sẽ làm thay đổi tần số alen theo hướng tăng tần số alen a và giảm tần số alen A.

P ⇒ Q: “ Nếu tam giác ABC có hai góc bằng 60o thì ABC là một tam giác đều”
Giả thiết: “Tam giác ABC có hai góc bằng 60o ”
Kết luận: “ABC là một tam giác đều”
Phát biểu lại định lí này dưới dạng điều kiện cần: “ABC là một tam giác đều là điều kiện cần để tam giác ABC có hai góc bằng 60o”
Phát biểu lại định lí này dưới dạng điều kiện đủ : “Tam giác ABC có hai góc bằng 60o là điều kiện đủ để ABC là tam giác đều”

tính chất nào có thể phát biểu thành định lí
1. Quan hệ giữa tính vuông góc và tính song song của ba đường thẳng
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
2. Ba đường thẳng song song
Hai đường thẳng phân biệt cùng song song với một đường thẳng thiws ba thì chúng cùng song song với nhau.
Ba đường thẳng d, d', d'' song song với nhau từng đôi một thì ta nói đường 3 thẳng ấy song song với nhau.