Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
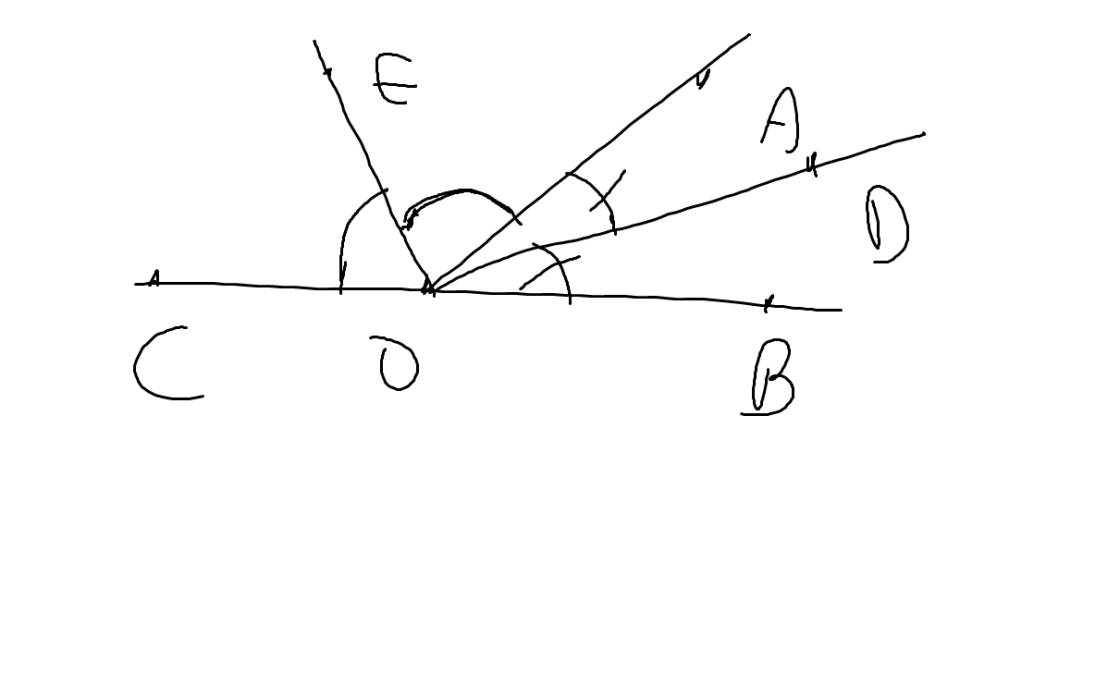
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)

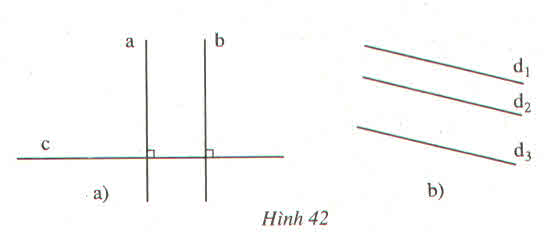
Nếu hai đường thằng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.

Hoặc: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó sẽ vuông góc với đường thẳng còn lại .
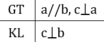

Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
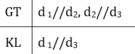

Bài 1:
| GT | \(\widehat{A}+\widehat{B}=90^0;\widehat{C}+\widehat{B}=90^0\) |
| KL | \(\widehat{A}=\widehat{C}\) |
Ta có: \(\widehat{A}+\widehat{B}=90^0\)
nên \(\widehat{A}=90^0-\widehat{B}\left(1\right)\)
Ta có: \(\widehat{C}+\widehat{B}=90^0\)
nên \(\widehat{C}=90^0-\widehat{B}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{C}\)
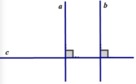

Tính chất có thể phát biểu thành định lí:
Nếu một đường thẳng cắt hai đường thẳng và trong số các hóc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.
Giả thuyết:
một đường thẳng cắt hai đường thẳng và trong số các góc tạo thành có một cặp góc so le trong bằng nhau.
Kết luận:
hai đường thẳng đó song song với nhau.