Biết x4-3x=90
Tính giá trị biểu thức A=x8-6x5+x4+9x3-3x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$

\(a,x^4-2x^3+6x^2+x+14\\ =\left(x^4-3x^3+7x^2\right)+\left(x^3-3x^2+7x\right)+\left(2x^2-6x+14\right)\\ =\left(x^2-3x+7\right)\left(x^2+x+2\right):\left(x^2-3x+7\right)=x^2+x+2\)
Ta có \(x^2+x+2=x^2+x+\dfrac{1}{4}+\dfrac{7}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}>0\)
Vậy ...
\(b,A=x^3+3xy+y^3\\ A=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\\ A=x^2-xy+y^2+3xy\\ A=x^2+2xy+y^2=\left(x+y\right)^2=1\)

\(a,n^3-2n^2+3n+3=n^3-n^2-n^2+n+2n-2+5\\ =\left(n-1\right)\left(n^2-n+2\right)+5\\ \Leftrightarrow n^3-2n^2+3n+3⋮\left(n-1\right)\\ \Leftrightarrow5⋮n-1\\ \Leftrightarrow n-1\in\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)
\(b,\Leftrightarrow x^4+6x^3+7x^2-6x+a\\ =x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1-1+a\\ =\left(x^2+3x-1\right)\left(x^2+3x-1\right)-1+a\\ =\left(x^2+3x-1\right)^2+a-1\)
Để \(x^4+6x^3+7x^2-6x+a⋮x^2+3x-1\)
\(\Leftrightarrow a-1=0\Leftrightarrow a=1\)

Thay x = -1 và đa thức, ta có:
(-1)2 + (-1)4 + (-1)6 + … + (-1)100 = 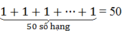
Vậy giá trị đa thức bằng 50 tại x = -1.

Ta thấy x=0 ko tm bài toán => x khác 0
Có : x^2-3x+1 = 0
=> x^2+1 = 3x
=> x^2+1/x = 3x/x = 3
=> x+1/x = 3
=> (x+1/x)^2 = 9
=> x^2+1/x^2+2=9
=> x^2+1/x^2 = 9-2 = 7
=> (x^2+1/x^2)^2 = 49
=> x^4+1/x^4+2 = 49
=> x^4+1/x^4 = 49-2 = 47
Vậy x^4+1/x^4 = 47
Tk mk nha

\(x^4-9x^3+21x^2+x+a=\left(x^2-8x+15\right)\left(x^2-x-2\right)+a+30\)
\(\Rightarrow a+30=0\Rightarrow a=-30\)

Ta có: \(M=x^4-xy^3+xy^3-y^4-1\)
\(=x^4-y^4-1\)
\(=\left(x^2-y^2\right)\left(x^2+y^2\right)-1\)
\(=\left(x+y\right)\left(x-y\right)\left(x^2+y^2\right)-1\)(1)
Thay x+y=0 vào biểu thức (1), ta được:
\(M=0-1=-1\)
Vậy: Khi x+y=0 thì M=-1
`M=x^4-xy^3+xy^3-y^4-1`
`=x(x^3+y^3)-y^3(x+y)-1`
`=x(x+y)(x^2-xy+y^2)-0-1`(do `x+y=0`)
`=0-0-1`
`=-1`

\(a,10x^2y-20xy^2=10xy\left(x-2y\right)\\ b,x^2-y^2+10y-25=x^2-\left(y^2-10y+25\right)=x^2-\left(y-5\right)^2=\left(x-y+5\right)\left(x+y-5\right)\\ c,x^2-y^2+3x-3y=\left(x-y\right)\left(x+y\right)+3\left(x-y\right)=\left(x-y\right)\left(x+y+3\right)\\ d,x^3+3x^2-16x-48=\left(x^3+3x^2\right)-\left(16x+48\right)=x^2\left(x+3\right)-16\left(x+3\right)=\left(x+3\right)\left(x^2-16\right)=\left(x+3\right)\left(x+4\right)\left(x-4\right)\)
\(e,9x^3+6x^2+x=x\left(9x^2+6x+1\right)=x\left(3x+1\right)^2\\ f,x^4+5x^3+15x-9=\left(x^4+5x^3-3x^2\right)+\left(3x^2+15x-9\right)=x^2\left(x^2+5x-3\right)+3\left(x^2+5x-3\right)=\left(x^2+3\right)\left(x^2+5x-3\right)\)

b. Ta có:
A(x) + B(x) = x2 + 2x + 1 + x2 + 1 = 2x2 + 2x + 2 (0.5 điểm)
A(x) - B(x) = x2 + 2x + 1 - (x2 + 1) = 2x (0.5 điểm)