Cho chóp S.ACB,SA⊥(ABC),ΔABC cân tại B,SA=a,góc ABC=120 độ,góc giữa (SBC) và (ABC) là 60 độ.Tính V chóp ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 3 2023
\(SB=\sqrt{\left(a\sqrt{3}\right)^2+a^2}=2a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
(SBC;ABC)=(SB;BA)=góc SBA=60 độ
CM
11 tháng 2 2017
Chọn A.
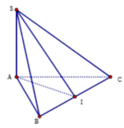
Gọi I là trung điểm của BC, tam giác ABC vuông cân tại A nên AI ⊥ BC
Có SA ⊥ (ABC) => SA ⊥ BC
Suy ra BC ⊥ (SAI). Suy ra ((SBC);(ABC)) = SIA.
∆ SIA vuông tại A có SA = a, AI = a. Suy ra vuông cân tại A.
Suy ra SIA = 45 °
CM
17 tháng 6 2018
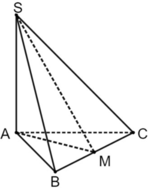
Có S B , A B C = ∠ S B A = 60 °
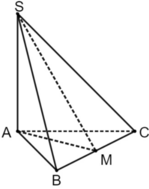
Gọi M là trung điểm BC, khi đó
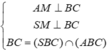
⇒ S B C , A B C = ∠ S M A
Có c o s ∠ S M A
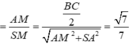
Chọn đáp án B.
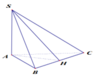
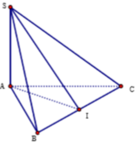
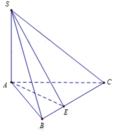
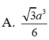
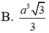
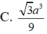
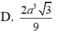
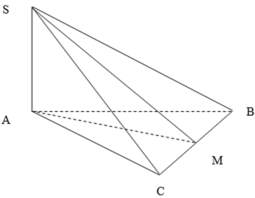
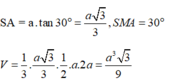
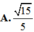
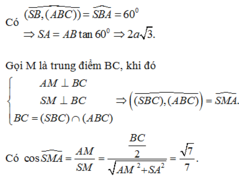
Kẻ AD vuông góc BC
\(\Rightarrow BC\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SBC) và (ABC)
\(\Rightarrow\widehat{SDA}=60^0\)
\(\Rightarrow AD=\dfrac{SA}{tan60^0}=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow AB=\dfrac{AD}{sin\widehat{ABD}}=\dfrac{AD}{sin60^0}=\dfrac{2a}{3}\)
\(V=\dfrac{1}{3}SA.S_{ABC}=\dfrac{1}{3}.a.\dfrac{1}{2}.\left(\dfrac{2a}{3}\right)^2.sin120^0=\dfrac{a^3\sqrt{3}}{27}\)