Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
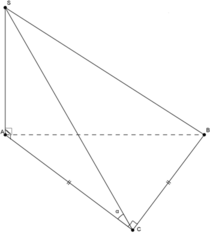
Ta có BC ⊥ AC và BC ⊥ SC, do đó góc giữa mp (SBC) và mp (ABC) chính là góc SCA.
Mặt khác
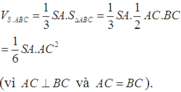
Vì tam giác SAC vuông tại A nên ta có
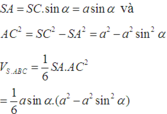
đặt t = sin α ta có hàm số thể tích theo t như sau
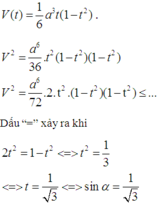

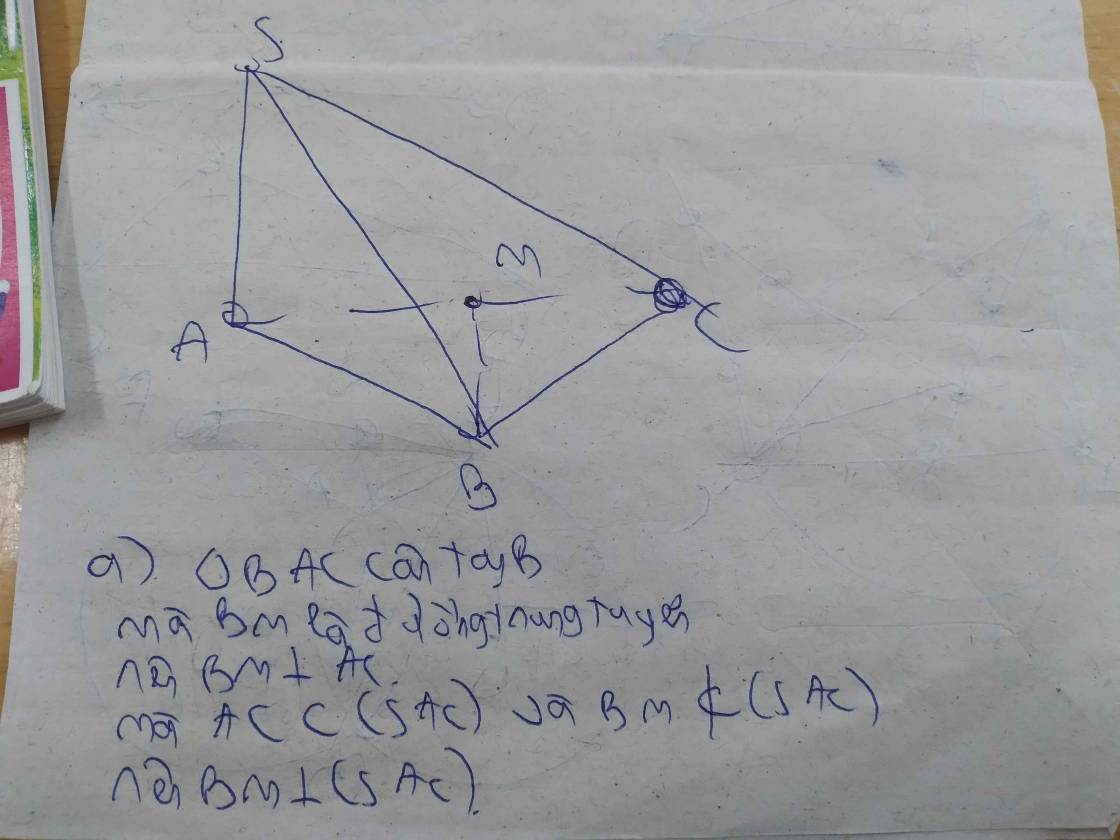
a.
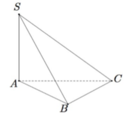
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)

c.
Từ M kẻ \(MH\perp SC\) (H thuộc SC)
\(\Rightarrow H\in\left(\alpha\right)\Rightarrow\) thiết diện là tam giác BMH
Do \(\left\{{}\begin{matrix}BM\perp\left(SAC\right)\\MH\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow BM\perp MH\Rightarrow\Delta BMH\) vuông tại M
Trong tam giác vuông ABC: \(BM=\dfrac{1}{2}AC=a\) (trung tuyến ứng với cạnh huyền)
Hai tam giác vuông CHM và CAS đồng dạng (chung góc C)
\(\Rightarrow\dfrac{MH}{SA}=\dfrac{CM}{SC}\Rightarrow MH=\dfrac{SA.CM}{SC}=\dfrac{SA.\dfrac{AC}{2}}{\sqrt{SA^2+AC^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\Rightarrow S_{BMH}=\dfrac{1}{2}BM.MH=\dfrac{a^2\sqrt{5}}{10}\)
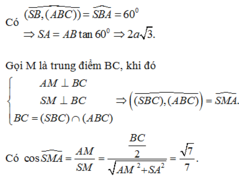

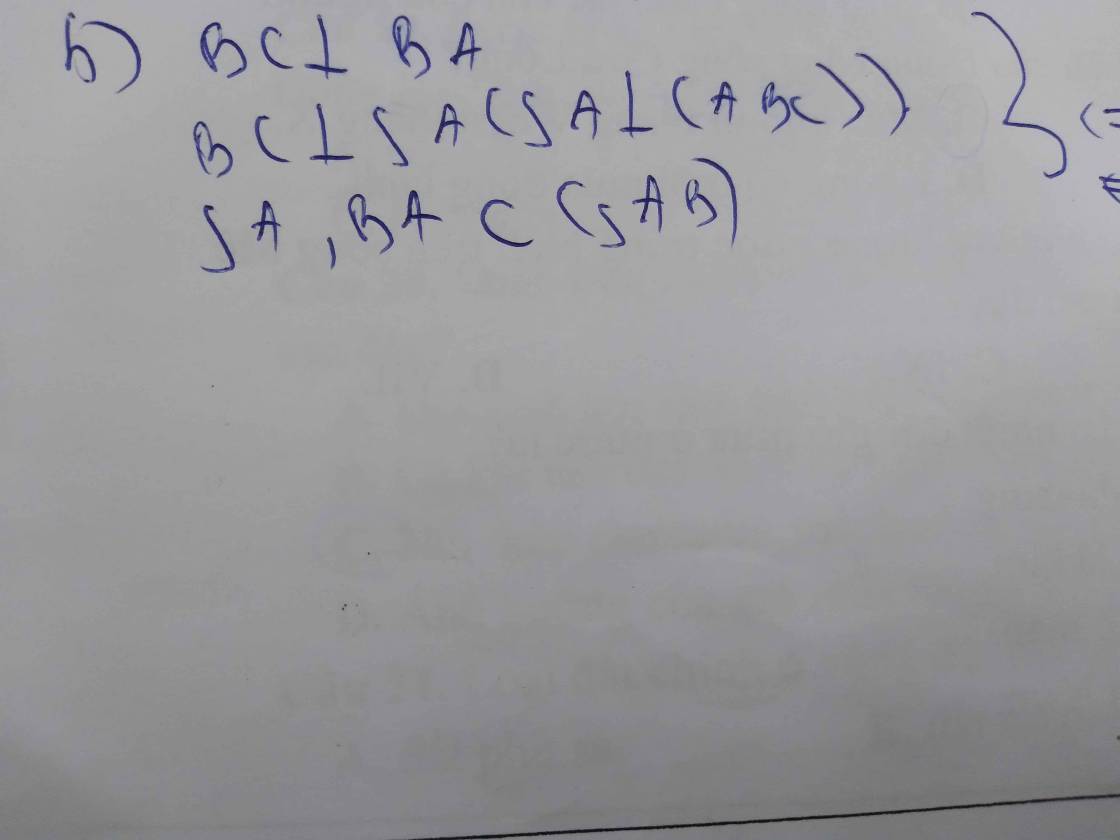

\(SB=\sqrt{\left(a\sqrt{3}\right)^2+a^2}=2a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
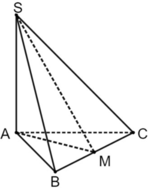
(SBC;ABC)=(SB;BA)=góc SBA=60 độ