
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để M nguyên thì \(5⋮\sqrt{a}+1\)
\(\Leftrightarrow\sqrt{a}+1\in\left\{1;5\right\}\)
\(\Leftrightarrow\sqrt{a}\in\left\{0;4\right\}\)
hay \(a\in\left\{0;16\right\}\)


Tham khảo: Cho tứ giác ABCD có góc C + góc D = 90 độ. Gọi M, N, P, Q theo thứ tự là trung điểm của AB, BD, DC, CA. Chứng minh 4 điểm M, N, P, Q cùng nằm trên 1 đường tròn - Toán học Lớp 9 - Bài tập Toán học Lớp 9 - Giải bài tập Toán học Lớp 9 | Lazi.vn - Cộng đồng Tri thức & Giáo dục


Xét ΔABD có
M là trung điểm của AB
S là trung điểm của AD
Do đó: MS là đường trung bình của ΔBAD
Suy ra: MS//BD và \(MS=\dfrac{BD}{2}\left(1\right)\)
mà BD\(\perp\)AC
nên MS\(\perp\)AC
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC
và AC\(\perp\)MS
nên MN\(\perp\)MS
Xét ΔBCD có
N là trung điểm của BC
R là trung điểm của CD
Do đó: RN là đường trung bình của ΔBCD
Suy ra: RN//BD và \(RN=\dfrac{BD}{2}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra MS//NR và MS=NR
Xét tứ giác MSRN có
MS//NR
MS=NR
Do đó: MSRN là hình bình hành
mà \(\widehat{SMN}=90^0\)
nên MSRN là hình chữ nhật
Suy ra: M,S,R,N cùng thuộc 1 đường tròn

a/ Vì tb đang xếp thành 1 hàng => tb đang ở kì giữa NP hoặc GP2
Nếu ở Kì giữa NP => 2n = 24
Nếu ở KÌ giữa GP 2 => 2n = 48
b/ Vì các NST kép đang phân li về 2 cực => Tb đang ở kì sau GP1 => 2n = 32

câu 3.
Ta biết rằng khi chuyển đổi từ \(^oC->^oF\) ta có công thức
\(y=ax+b\)(trong đó x là số chỉ \(^oC\), y là chỉ \(^oF\))
theo bài ra=>hệ pt:\(\left\{{}\begin{matrix}32=a.0+b\\212=100a+b\end{matrix}\right.< =>\left\{{}\begin{matrix}b=32\\a=1,8\end{matrix}\right.\)
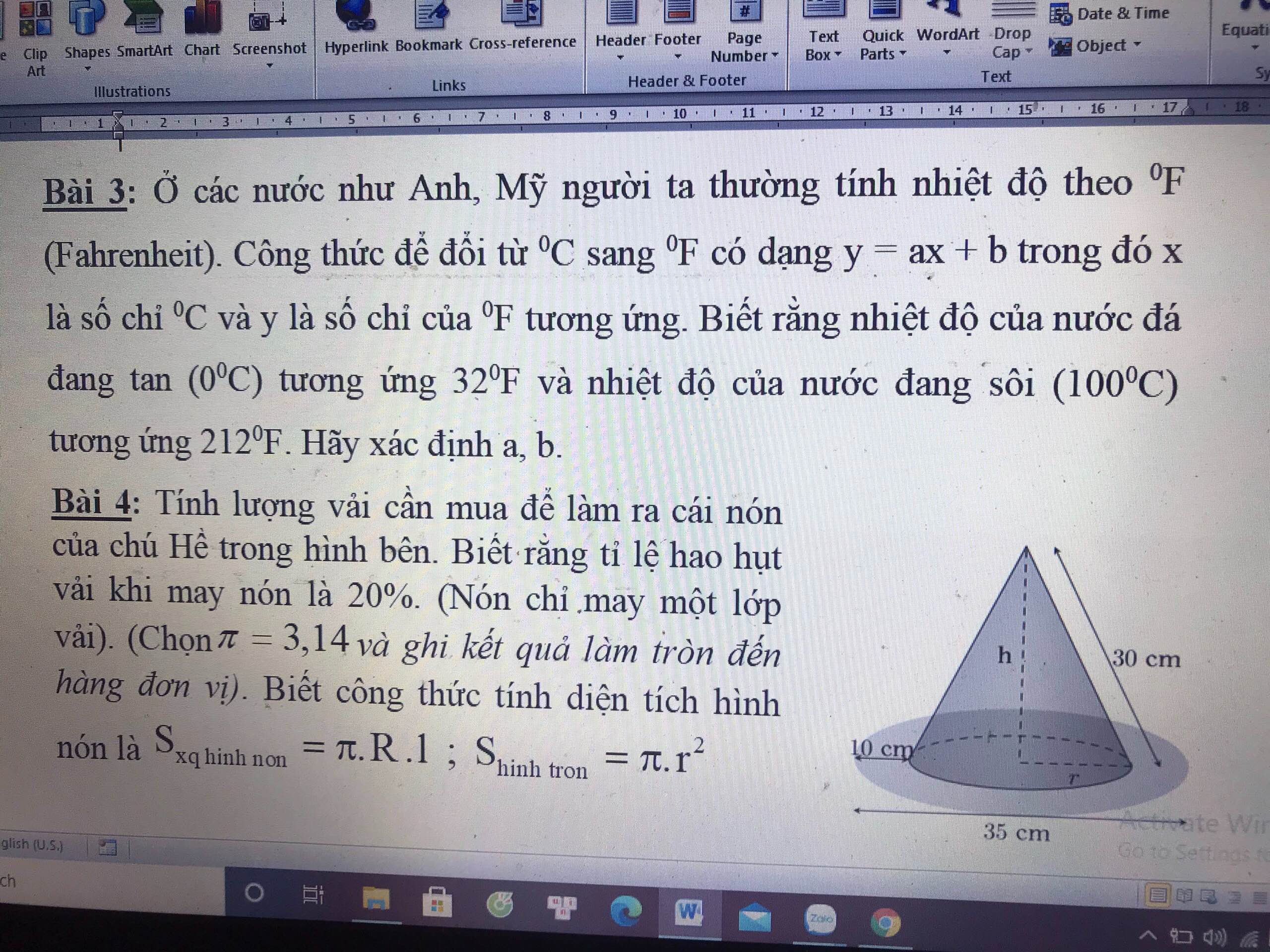
câu 4:
đường kính nón : \(35-10-10=15cm\)
=>bán kính nón: \(R=\dfrac{15}{2}=7,5cm^{ }\)
=>Sxq(nón)=\(\pi Rl=3,14.30.7,5\approx707cm^2\)
S(vành nón)=\(\pi\left(\dfrac{35}{2}\right)^2-\pi.\left(\dfrac{15}{2}\right)^2=785cm^2\)
S(vải cần thiết)=\(707+785=1492cm^2\)
do hao hụt 20% vải nên số vải cần để khâu mũ là:
\(1492+20\%.1492\approx1790cm^2\)




a) xét tg ABD và tg ACD có :
AB = AC (gt)
AD chung
Góc BAC = góc DAC( AD là p/g góc BAC)
=> tg ABD = tg ADC( c-g-c)
b)xét tg AMB và tg AMC có:
AM chung
AB = AC (gt)
góc BAM = góc CAM ( M thuộc AD)
=> tg ABM = tg ACM ( c-g-c)
c)vì tg ADB = tg ADC (cmt)
=> DB = DC (cạnh tương ứng )
Vì tg AMB = tg AMC (cmt)
=> BM = MC (cạnh tương ứng)
Xét tg MBD và tg MCD có
MB= MC (cmt)
MD chung
BD = DC ( cmt)
=> tg MBD = tg MCD ( c-c-c)
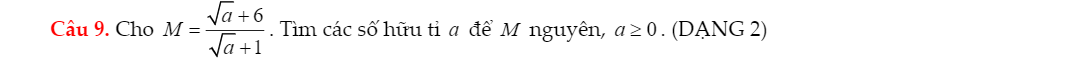

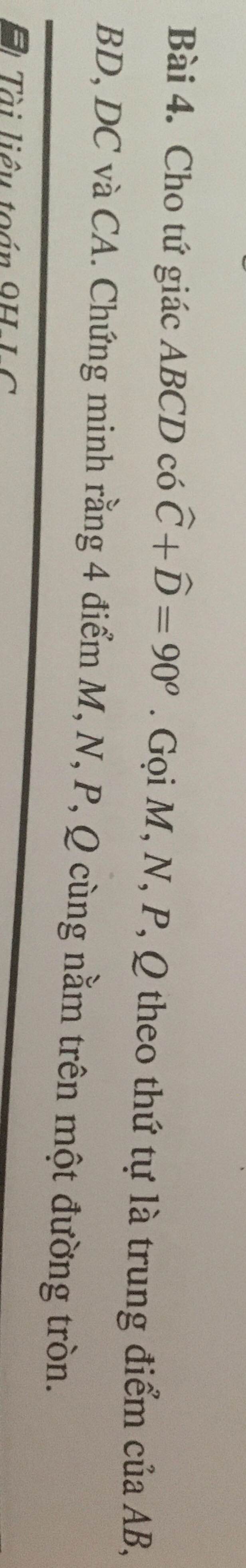


 giúp em bài này với ạ. Em cảm ơn
giúp em bài này với ạ. Em cảm ơn

