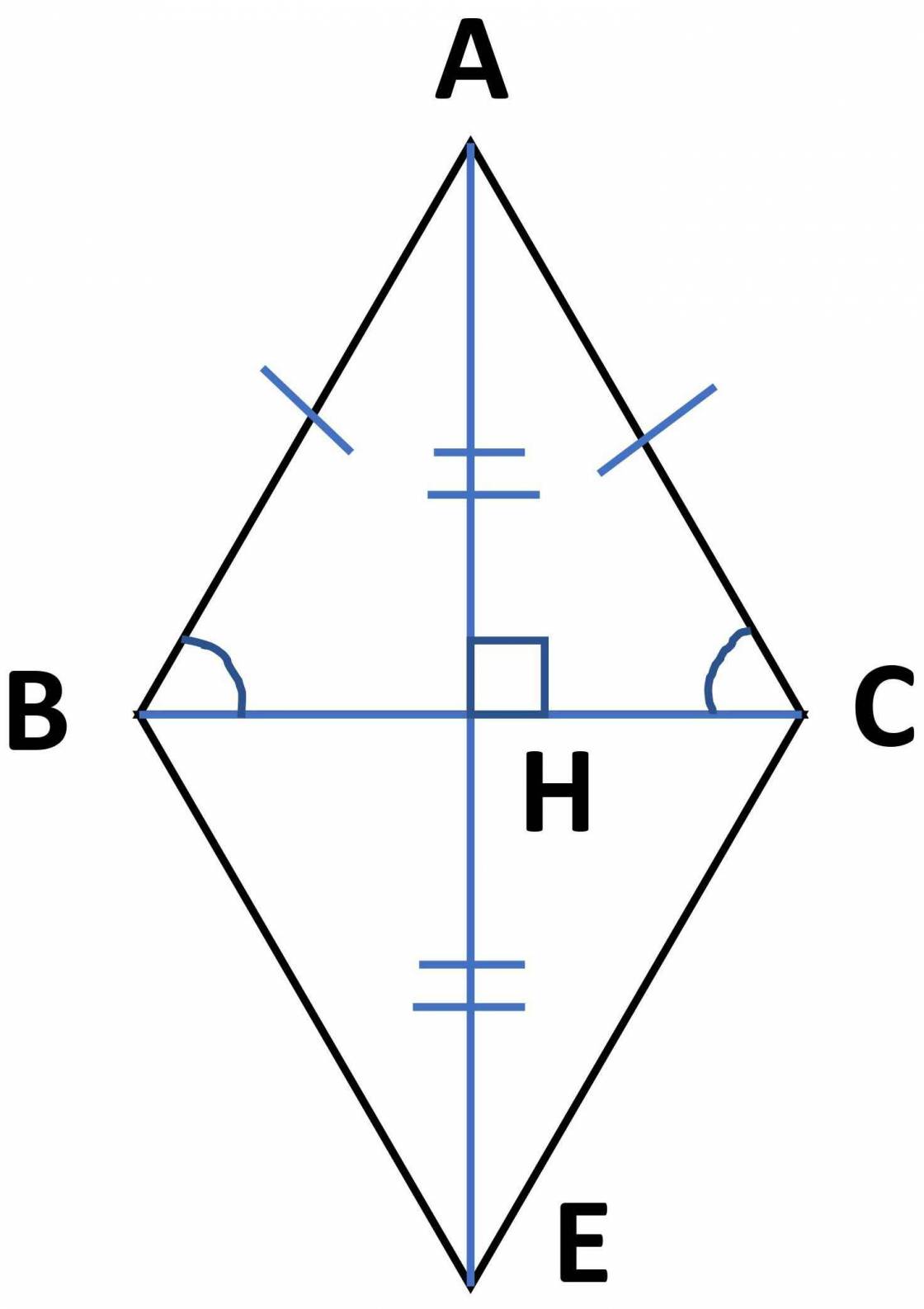
Cho tam giác ABC có AB=AC, H là trung điểm của BC. Trên tia đối của HA lấy K sao cho KH = AH. Chứng minh rằng
a, \(\Delta ABH=\Delta ACH\)
B, \(AH\perp BC\)
C, CK//AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 12 2021
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
4 tháng 12 2021
\(a,\left\{{}\begin{matrix}AB=AC\\BH=HC\\AH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AHB=\Delta AHC\left(c.c.c\right)\\ \Rightarrow\widehat{AHB}=\widehat{AHC}\\ \text{Mà }\widehat{AHB}+\widehat{AHC}=180^0\\ \Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\\ \Rightarrow AH\perp BC\\ b,\left\{{}\begin{matrix}HM=HA\\\widehat{AHB}=\widehat{MHC}\left(đđ\right)\\BH=HC\end{matrix}\right.\Rightarrow\Delta AHB=\Delta MHC\left(c.g.c\right)\\ \Rightarrow\widehat{HBA}=\widehat{HCM}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}MC\)
VN
22 tháng 12 2016
a) Xét tam giác ABC có AB = AC => Tam giác ABC cân tại A
=> AH vừa là đường trung tuyến vừa là tia phân giác góc BAC
b) Vì tam giác ABC cân tại A (cmt)
=> AH cũng là đường cao
=> AH vuông góc BC
c) Xét tứ giác ABCK có
H là trung điểm BC (gt)
H là trung điểm AK (gt)
=> Tứ giác ABCK là hình bình hành
=> CK // AB
PT
22 tháng 12 2016
a) Xét tam giác AHB và tam giác AHC có :
AB=AC ( gt )
BH = HC ( vì H là trung điểm của cạnh BC )
AH : cạnh chung
do đó tam giác AHB = tam giác AHC ( c.c.c )
suy ra góc BAH = HAC ( 2 góc t/ứ )
nên AH là tia phân giác của góc BAC
b) Có tam giác AHB = tam giác AHC ( c/m trên )
suy ra góc BHA = góc CHA ( 2 góc t/ứ )
mà B , H , C thẳng hàng
suy ra góc BHC là góc bẹt
suy ra góc BHA = góc CHA = 90 độ
nên AH vuông góc với BC
cám ơn bn nhìu
15 tháng 7 2016
a, Xét tam gác ABH và tam giác ACH có:
AB=AC (gt)
BH=CH
AH là cạnh chung
=> tam giác ABH=ACH ( c.c.c)
=> góc BAH = CAH ( hai góc tương ứng )
Vì tam giác ABC là tam giác cân mà AH vừa là trung điểm vừa là tia phân giác thì AH cũng là đường cao của ta giác ABC => AH vuông góc vs BC
b, Xét tam giác vuông ABH và tam giác vuông KCH có :
BH=CH (gt)
HK=HA (gt)
=> tam giác vuông ABH = tam giác vuông KCH ( hai cạnh góc vuông )
=> góc HAB = góc HKC ( hai góc tương ứng )
Vì góc HAB = góc HKC nên CK//AB ( cặp góc sole trong )
S
19 tháng 12 2022
a) xét ΔABH và ΔACH, ta có :
AB = AC (giả thiết)
\(\widehat{ABC}=\widehat{ACB}\) (vì AB = AC => đó là tam giác cân, mà tam giác cân thì có 2 góc ở đáy bằng nhau)
AH là cạnh chung
ð ΔABH = ΔACH (c.c.c)
b) vì ΔABH = ΔACH, nên :
=> HB = HC (2 cạnh tương ứng)
c) hơi khó nha !
5 tháng 11 2017
a, vì AH là trung diểm của BC nên ∆ABH=∆ACH
b,∆ABH=∆ACH và AH là trung diểm của BC nên AH vuông góc với BC
c,vì AH vuông góc với BC và ∆ABH=∆ACH => CK//AB
( hình vẽ và GTKL tự làm)
a) xét \(\Delta ABH\)và\(\Delta ACH\)có :
\(AB=AC\)\(\left(GT\right)\)
\(BH=CH\left(GT\right)\)\(\Rightarrow\Delta ABH=\Delta ACH\left(c.c.c\right)\)
\(AH\)\(chung\)
b) Ta có \(AHB=AHC\)( 2 góc tương ứng )
.Mà \(AHB+AHC=180\)O
\(\Rightarrow AHB=AHC=90\)O
\(\Rightarrow AH\perp BC\)
C) Xét 2 \(\Delta AHB\)và\(KHC\)có :
\(BH=CH\)\(\left(GT\right)\)
\(KH=AH\left(GT\right)\)
\(BHA=CHK\)( ĐỐI ĐỈNH )
\(\Rightarrow\Delta AHB=\Delta KHC\left(c.g.c\right)\)
\(\Rightarrow ABH=KCH\)( 2 góc tương ứng )
Mà 2 góc này so le trong
\(\Rightarrow CK//AB\)