Lập phương trình đường trung trực của đoạn thẳng AB biết A (1,2); B (2,4)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 4 2021
Đường thẳng AB nhận \(\overrightarrow{n}=\left(1;2\right)\) làm vecto pháp tuyến
AB đi qua A (1; -1) nên nó có phương trình là
x - 1 + 2 (y + 1) = 0 hay x + 2y + 1 = 0
Gọi M là trung điểm của AB ⇒ M ∈ Δ, tọa độ của M có dạng
M (t ; 2t + 1) với t là số thực và \(\overrightarrow{AM}=\left(t-1;2t+2\right)\)
⇒ AM ⊥ Δ
⇒ \(\overrightarrow{AM}.\overrightarrow{n}=0\)
⇒ t + 1 + 2. (2t + 2) = 0
⇒ t = -1
Vậy M (- 1; - 1)
M là trung điểm của AB => Tọa độ B
Làm tương tự như thế sẽ suy ra tọa độ C
HQ
Hà Quang Minh
Giáo viên
29 tháng 9 2023
a) Phương trình đường thẳng AB đi qua 2 điểm A và B là: \(\frac{{x - 1}}{{ - 1 - 1}} = \frac{{y - 3}}{{ - 1 - 3}} \Leftrightarrow \frac{{x - 1}}{{ - 2}} = \frac{{y - 3}}{{ - 4}} \Leftrightarrow 2x - y + 1 = 0\)
Phương trình đường thẳng AC đi qua 2 điểm A và C là: \(\frac{{x - 1}}{{5 - 1}} = \frac{{y - 3}}{{ - 3 - 3}} \Leftrightarrow \frac{{x - 1}}{4} = \frac{{y - 3}}{{ - 6}} \Leftrightarrow 3x + 2y - 9 = 0\)
Phương trình đường thẳng BC đi qua 2 điểm B và C là:
\(\frac{{x + 1}}{{5 + 1}} = \frac{{y + 1}}{{ - 3 + 1}} \Leftrightarrow \frac{{x + 1}}{6} = \frac{{y + 1}}{{ - 2}} \Leftrightarrow x + 3y + 4 = 0\)
b) Gọi d là đường trung trực của cạnh AB.
Lấy N là trung điểm của AB, suy ra \(N\left( {0;1} \right)\).
Do \(d \bot AB\) nên ta có vecto pháp tuyến của d là: \(\overrightarrow {{n_d}} = \left( {1;2} \right)\)
Vậy phương trình đường thẳng d đi qua N có vecto pháp tuyến \(\overrightarrow {{n_d}} = \left( {1;2} \right)\) là:
\(1\left( {x - 0} \right) + 2\left( {y - 1} \right) = 0 \Leftrightarrow x + 2y - 2 = 0\)
c) Do AH vuông góc với BC nên vecto pháp tuyến của AH là \(\overrightarrow {{n_{AH}}} = \left( {3; - 1} \right)\)
Vậy phương trình đường cao AH đi qua điểm A có vecto pháp tuyến \(\overrightarrow {{n_{AH}}} = \left( {3; - 1} \right)\)là: \(3\left( {x - 1} \right) - 1\left( {y - 3} \right) = 0 \Leftrightarrow 3x - y = 0\)
Do M là trung điểm BC nên \(M\left( {2; - 2} \right)\). Vậy ta có: \(\overrightarrow {AM} = \left( {1; - 5} \right) \Rightarrow \overrightarrow {{n_{AM}}} = \left( {5;1} \right)\)
Phương trình đường trung tuyến AM đi qua điểm A có vecto pháp tuyến \(\overrightarrow {{n_{AM}}} = \left( {5;1} \right)\) là:
\(5\left( {x - 1} \right) + 1\left( {y - 3} \right) = 0 \Leftrightarrow 5x + y - 8 = 0\)
CM
21 tháng 6 2017
Đáp án C
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB. Ta có
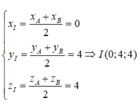
Ta chọn:
Vậy phương trình của mặt phẳng (P) là:
-2(x - 0) + 2(y - 4) - 2(z - 4) = 0 ⇔ -2x + 2y - 2z = 0 ⇔ x - y + z = 0
Vậy đáp án đúng là C.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
\(\overrightarrow{AB}=\left(4;4\right)=4\left(1;1\right)\)
Đường trung trực của AB vuông góc AB nên nhận \(\left(1;-1\right)\) là 1 vtcp
Gọi M là trung điểm AB \(\Rightarrow M\left(1;3\right)\)
Phương trình trung trực AB qua M có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=3-t\end{matrix}\right.\)
CM
11 tháng 8 2017
Gọi M trung điểm của AB nên M( 2; 1)
Ta có 
Gọi d là đường thẳng trung trực của AB
thì d qua M(2; 1) và nhận 
làm VTPT.
Phương trình đường thẳng d là:
1( x- 2) – 6.(y -1) =0
Hay x- 6y+ 4= 0.
Chọn D