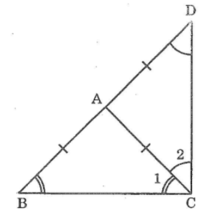
Cho tam giác ABC cân tại A , vẽ D sao cho A là trung điểm của BD . Tính số đo góc BCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: ∆ABC cân tại A
⇒ AB = AC và ∠B = ∠C1 (tính chất tam giác cân) (1)
Lại có: AD = AB ( do A là trung điểm BD).
Suy ra: AD = AC do đó ∆ACD cân tại A
Nên ∠D =∠C2(tính chất tam giác cân) (2)
Mà ∠BCD =∠C1+ ∠C2 (3)
Từ (1); (2) và (3) suy ra: ∠BCD =∠B +∠D (4)
Trong ∆BCD, ta có:
∠BCD +∠B +∠D =180o (tổng 3 góc trong tam giác) (5)
từ (4) và (5) suy ra : 2 ∠BCD =180° hay∠BCD =90°

Hình vẽ:
A B C D
Giải:
Ta có: \(AB=\dfrac{BD}{2}\) ( \(A\) là trung điểm của \(BD\) )
Mà \(AB=AC\) ( Vì tam giác \(ABC\) cân tại \(A\) )
\(\Rightarrow AC=\dfrac{BD}{2}\)
Mà \(AC\) là đường trung tuyến của tam giác \(CBD\) ( \(A\) là trung điểm của\(BD \) ).
\(\Rightarrow\Delta CBD\) vuông tại \(C.\)
\(\Rightarrow\widehat{BCD}=90^o\)
Vì AC = AD
\(\Rightarrow\Delta ACD\) cân ại A
\(\Rightarrow\widehat{ACD}=\widehat{ADC}\) (1)
Vì \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\) (2)
\(\Delta BDC\) có :
\(\widehat{ABC}+\widehat{ACB}+\widehat{DCA}+\widehat{CDA}=180^0\)
Từ (1) và (2)
\(\Rightarrow\widehat{ABC}+\widehat{ADC}=\widehat{ACB}+\widehat{DCA}\)
\(\Rightarrow\left(\widehat{ACB}+\widehat{DCA}\right)\times2=180^0\)
\(\Rightarrow\widehat{ACB}+\widehat{DCA}=180^0\times\dfrac{1}{2}=90^0\)
\(\Rightarrow\widehat{BCD}=90^0\)
![]()
![]()
![]()

Ta có AB=AD nên CA là đường trung tuyến:
Suy ra tam giác BCD vuông tại C Suy ra góc BCD=90 độ
A B C D Ta có AB=AD nên CA là đường trung tuyến =>tam giác BCD vuông tại C => góc BCD =90 độ

A B C D
Có tam giác ABC cân tại A (gt)
=> AB = AC
Có A là trung điểm BD (gt)
=> AB = AD
=> AC = AD (= AB)
=> AC = \(\frac{1}{2}\)BD (= AB = AD)
Có A là trung điểm BD (gt)
=> CA là trung tuyến tam giác BDC
Mà CA = \(\frac{1}{2}\)BD (cmt)
=> tam giác BDC vuông tại C (đảo định lí trung tuyến ứng với cạnh huyền trong tam giác vuông)
=> góc BCD = 90o
Hình Giang vẽ rồi, tớ làm cách khác =)))
Tam giác ABC cân tại A \(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{ABC}=\widehat{ACB}\left(1\right)\end{cases}}\)
A là trung điểm của BD => AB=AD mà AB=AC => AD=AC
=> Tam giác CAD cân tại A => \(\widehat{ADC}=\widehat{ACD}\)(2)
Từ (1) và (2) => \(\widehat{ABC}+\widehat{ADC}=\widehat{ACB}+\widehat{ACD}=\widehat{BCD}\)
Tam giác BDC có: \(\widehat{ABC}+\widehat{ADC}+\widehat{BCD}=180^o\)(tổng 3 góc trong tam giác) =>\(\widehat{BCD}=\frac{180^o}{2}=90^o\)