Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

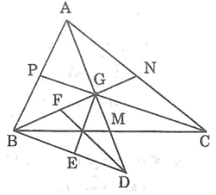
a. Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.
Ta có: AG = GD (gt)
AG = 2GM (tính chất đường trung tuyến)
Suy ra: GD = 2GM
Mà GD = GM + MD ⇒ GM = MD
Xét ΔBMD và ΔCMG, ta có:
BM = CM (gt)
∠(BMD) = ∠(CMG) (đối đỉnh)
MD = GM (chứng minh trên)
Suy ra: ΔBMD = ΔCMG (c.g.c)
⇒ BD = CG (hai cạnh tương ứng)
Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)
Suy ra: BD = 2/3 CP (1)
Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)
Và AG = 2/3 AM (tính chất đường trung tuyến)
Suy ra: GD = 2/3 AM (3)
Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.
b. Ta có: GM = MD (chứng minh trên)
Suy ra BM là đường trung tuyến của tam giác BGD.
Suy ra: BM = 1/2 BC (4)
Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:
FG = 1/2 BG (tính chất đường trung tuyến)
GN = 1/2 GB (tính chất đường trung tuyến)
Suy ra: FG = GN
Xét ΔDFG và ΔANG, ta có:
AG = GD (gt)
∠(DGF) = ∠(AGN) (đối đỉnh)
GF = GN (chứng minh trên)
Suy ra: ΔDFG = ΔANG (c.g.c) ⇒ DF = AN
Mà AN = 1/2 AC (gt)
Suy ra: DF = 1/2 AC (5)
Mặt khác: BD = CG (chứng minh trên)
ED = 1/2 BD (vì E là trung điểm BD)
GP = 1/2 CG (tính chất đường trung tuyến)
Suy ra: ED = GP
Lại có: ΔBMD = ΔCMG (chứng minh trên)
⇒ ∠(BDM) = ∠(CGM) hay ∠(EDG) = ∠(CGM)
(CGM) = (PGA) (đối đỉnh)
Suy ra: ∠(EDG) = ∠(PGA)
AG = GD (gt)
Suy ra: ΔPGA = ΔEDG (c.g.c) ⇒ GE = AP mà AP = 1/2 AB (gt)
Do đó: GE = 1/2 AB(6)
Từ (4), (5) và (6) suy ra các đường trung tuyến của ΔBGD bằng một nửa cạnh của ΔABC.

Hình vẽ:
A B C D
Giải:
Ta có: \(AB=\dfrac{BD}{2}\) ( \(A\) là trung điểm của \(BD\) )
Mà \(AB=AC\) ( Vì tam giác \(ABC\) cân tại \(A\) )
\(\Rightarrow AC=\dfrac{BD}{2}\)
Mà \(AC\) là đường trung tuyến của tam giác \(CBD\) ( \(A\) là trung điểm của\(BD \) ).
\(\Rightarrow\Delta CBD\) vuông tại \(C.\)
\(\Rightarrow\widehat{BCD}=90^o\)
Vì AC = AD
\(\Rightarrow\Delta ACD\) cân ại A
\(\Rightarrow\widehat{ACD}=\widehat{ADC}\) (1)
Vì \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\) (2)
\(\Delta BDC\) có :
\(\widehat{ABC}+\widehat{ACB}+\widehat{DCA}+\widehat{CDA}=180^0\)
Từ (1) và (2)
\(\Rightarrow\widehat{ABC}+\widehat{ADC}=\widehat{ACB}+\widehat{DCA}\)
\(\Rightarrow\left(\widehat{ACB}+\widehat{DCA}\right)\times2=180^0\)
\(\Rightarrow\widehat{ACB}+\widehat{DCA}=180^0\times\dfrac{1}{2}=90^0\)
\(\Rightarrow\widehat{BCD}=90^0\)
![]()
![]()
![]()

Ta có AB=AD nên CA là đường trung tuyến:
Suy ra tam giác BCD vuông tại C Suy ra góc BCD=90 độ
A B C D Ta có AB=AD nên CA là đường trung tuyến =>tam giác BCD vuông tại C => góc BCD =90 độ
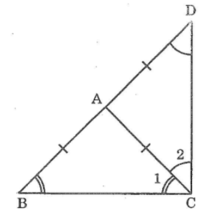



Ta có: ∆ABC cân tại A
⇒ AB = AC và ∠B = ∠C1 (tính chất tam giác cân) (1)
Lại có: AD = AB ( do A là trung điểm BD).
Suy ra: AD = AC do đó ∆ACD cân tại A
Nên ∠D =∠C2(tính chất tam giác cân) (2)
Mà ∠BCD =∠C1+ ∠C2 (3)
Từ (1); (2) và (3) suy ra: ∠BCD =∠B +∠D (4)
Trong ∆BCD, ta có:
∠BCD +∠B +∠D =180o (tổng 3 góc trong tam giác) (5)
từ (4) và (5) suy ra : 2 ∠BCD =180° hay∠BCD =90°