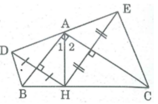
Cho \(\Delta ABC\) vuông tại A, đường cao AH. Vẽ điểm D đối xứng với H qua AB, điểm E đối xứng với H qua AC
a) Chứng minh BD = BH và BD \(\perp\) AD
b) Chứng minh BD + CE = BC
c) Chứng minh D, A, E thẳng hàng
d) Gọi M là trung điểm của BC. Chứng minh D đối xứng với E qua MA

a: Vì H và D đối xứng nhau qua AB
nên AH=AD; BH=BD
Xét ΔAHB và ΔADB có
AH=AD
HB=DB
AB chung
Do đó ΔAHB=ΔADB
Suy ra: góc ADB=90 độ và góc HAB=góc DAB
hay BD vuông góc với AD và AB là phân giác của góc HAD(1)
b: Ta có: H và E đối xứng nhau qua AC
nên AH=AE; CH=CE
=>ΔAHC=ΔAEC
=>góc AEC=90 độ và góc HAC=góc EAC
=>AC là phân giác của góc HAE(2)
Ta có: CH+BH=BC
=>BD+CE=BC
c: Từ (1) và (2) suy ra góc DAE=2x90=180 độ
=>D,A,E thẳng hàng