Cho 0^{\circ} < x < 90^{\circ} . Chứng minh đẳng thức sau :
\left ( \sqrt{\frac{1+sinx}{1-sinx}}-\sqrt{\frac{1-sinx}{1+sinx}} \right )^{2}= 4tan^{2}x |
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
9 tháng 10 2023
\( - 4^\circ C\): đọc là “âm bốn độ C” hoặc “trừ bốn độ C”
\( - 10^\circ C\): đọc là “âm mười độ C” hoặc “trừ mười độ C”
\( - 23^\circ C\): đọc là “âm hai mươi ba độ C” hoặc “trừ hai mươi ba độ C”.
23 tháng 3 2022
a) Ta có: \(sin^2x+sin^2\left(90-x\right)=sin^2x+cos^2x=1.\)
áp dụng: A = 2
b)Ta có: \(cos\left(x\right)=-cos\left(180-x\right)\)
áp dụng: B = 0
c) Ta có: \(tan\left(x\right)\cdot tan\left(90-x\right)=\frac{sinx}{cosx}\cdot\frac{sin\left(90-x\right)}{cos\left(90-x\right)}=\frac{sinx}{cosx}\cdot\frac{cosx}{sinx}=1\)
áp dụng: C = 1
7 tháng 3 2023
Vì Om là phân giác của \(\widehat{xOy}\)
\(\Rightarrow\widehat{IOE}=\widehat{IOF}=\dfrac{1}{2}\widehat{EOF}\)
Vì \(\left\{{}\begin{matrix}IE\perp Ox\\IF\perp Oy\end{matrix}\right.\left(gt\right)\Rightarrow\widehat{IEO}=\widehat{IFO}=90^o\)
Xét \(\Delta IOE\) và \(\Delta IOF\) có: \(\left\{{}\begin{matrix}\widehat{IEO}=\widehat{IFO}\left(=90^o\right)\\OI:chung\\\widehat{IOE}=\widehat{IOF}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta IOE=\Delta IOF\left(\text{cạnh huyền - góc nhọn}\right)\)
b) Vì \(\Delta IOE=\Delta IOF\left(cmt\right)\Rightarrow OE=OF\left(\text{2 cạnh tương ứng}\right)\)
Xét \(\Delta EOF\) có: \(OE=OF\left(cmt\right)\)
\(\Rightarrow\Delta EOF\) cân ở O
\(\Rightarrow\widehat{OEF}=\widehat{OFE}\)
Xét \(\Delta EOF\) có:
\(\widehat{EOF}+\widehat{OFE}+\widehat{OEF}=180^o\)
\(\Rightarrow2\widehat{EOI}+2\widehat{OEF}=180^o\\ \Rightarrow\widehat{EOI}+\widehat{OEF}=90^o\)
Gọi \(EF\cap OI\equiv M\)
Xét \(\Delta OME\) có:
\(\widehat{OEF}+\widehat{EOI}+\widehat{OME}=180^o\\ \Rightarrow90^o+\widehat{OME}=180^o\\ \Rightarrow\widehat{OME}=180^o-90^o=90^o\\ \Rightarrow EF\perp Om\left(\text{đpcm}\right)\)
18 tháng 4 2023
Cho , , là tia phân giác . Trên tia lấy điểm bất kì. Gọi lần lượt là chân đường vuông góc kẻ từ đến và . Chứng minh:
a) .
b) .
Hướng dẫn giải: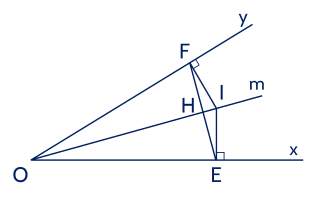
a) Xét và có
(giả thiết);
cạnh chung;
( là tia phân giác).
Vậy (cạnh huyền - góc nhọn).
b) (chứng minh trên)
(hai cạnh tương ứng).
Gọi là giao điểm của và .
Xét và , có
(chứng minh trên);
( là tia phân giác);
chung.
Do đó (c.g.c)
(hai góc tương ứng)
Mà nên .
Vậy .
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) Ta có: \(0= 1,8x + 32\)
\(\begin{array}{l} \Rightarrow 1,8x = - 32\\ \Rightarrow x = - 17,(7)\end{array}\)
Vậy \(0 ^\circ F\) tương ứng với \(-17,(7)^0C\)
b) \(T(35) = 1,8 . 35 + 32 = 95 (^\circ F )\)
Vậy nhiệt độ 35\(^\circ \)C tương ứng với 95 \(^\circ \)F
c) Ta có: \(41= 1,8x + 32\)
\(\begin{array}{l} \Rightarrow 1,8x = 41 - 32\\ \Rightarrow 1,8x = 9\\ \Rightarrow x = 5\end{array}\)
Vậy 41\(^\circ \)F tương ứng với 5\(^\circ \)C
24 tháng 8 2023
a) \(cos638^o=cos\left(-82^o\right)=cos\left(82^o\right)=sin8^o\)
b) \(cot\dfrac{19\pi}{5}=cot\dfrac{4\pi}{5}=-cot\dfrac{\pi}{5}\)
H9
HT.Phong (9A5)
CTVHS
22 tháng 7 2023
Ta có tổng 4 góc trong tứ giác là: \(360^o\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Hay: \(60^o+110^o+\widehat{C}+70^o=360^o\)
\(\Rightarrow\widehat{C}=360^o-\left(110^o+60^o+70^o\right)120^o\)
Vậy chọn đáp án A
H9
HT.Phong (9A5)
CTVHS
22 tháng 7 2023
Vì ABCD là hình thang cân
\(\Rightarrow\widehat{A}+\widehat{D}=180^o\)
Nên: \(\widehat{D}=180^o-\widehat{A}=180^o-65^o=115^o\)
Mặt khác ta có ABCD là hình thang cân nên:
\(\widehat{C}=\widehat{D}=115^o\)
Vậy chọn đáp án A
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
a) Điều kiện xác định là: \(x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
Vì tan0 = 0 nên phương trình tanx = 0 có các nghiệm \(x = k\pi ,{\rm{ }}k\; \in \;\mathbb{Z}.\)
Vậy tập nghiệm của phương trình là: \(S = \{ k\pi ,{\rm{ }}k\; \in \;\mathbb{Z}\} .\)
\(\begin{array}{*{20}{l}}{b){\rm{ }}tan\left( {30^\circ -3x} \right) = tan75^\circ }\\{ \Leftrightarrow \;tan\left( {3x-30^\circ } \right) = tan\left( {-{\rm{ }}75^\circ } \right)}\\{ \Leftrightarrow \;3x-30^\circ = -75^\circ + k360^\circ ,k\; \in \;\mathbb{Z}}\\{ \Leftrightarrow \;3x = -\,45^\circ + k360^\circ ,k\; \in \;\mathbb{Z}}\\{ \Leftrightarrow \;x = -15^\circ + k120^\circ ,k\; \in \;\mathbb{Z}.}\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \{ -15^\circ + k120^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}\} .\)
\(\begin{array}{l}{\rm{c, cos}}\left( {x + \frac{\pi }{{12}}} \right) = {\rm{cos}}\frac{{3\pi }}{{12}}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{{12}} = \frac{{3\pi }}{{12}} + k2\pi \\x + \frac{\pi }{{12}} = - \frac{{3\pi }}{{12}} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {\frac{\pi }{6} + k2\pi ; - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}} \right\}\)