Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,cos\left(\dfrac{21\pi}{6}\right)=cos\left(3\pi+\dfrac{\pi}{2}\right)=cos\left(\pi+\dfrac{\pi}{2}\right)=-cos\left(\dfrac{\pi}{2}\right)=0\\ b,sin\left(\dfrac{129\pi}{4}\right)=sin\left(32\pi+\dfrac{\pi}{4}\right)=sin\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\\ c,tan\left(1020^o\right)=tan\left(5\cdot180^o+120^o\right)=tan\left(120^o\right)=-\sqrt{3}\)

a) Ta có \( - {1485^ \circ } = - {45^ \circ } + ( - 4){.360^ \circ }\). Vậy điểm biểu diễn góc lượng giác có số đo \( - {1485^ \circ }\)là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ IV sao cho \(\widehat {AMO} = {45^ \circ }\)
b) Ta có \(\frac{{19\pi }}{4} = \frac{{3\pi }}{4} + 4\pi \). Vậy điểm biểu diễn góc lượng giác có số đo \(\frac{{19\pi }}{4}\) là điểm N trên phần đường tròn lượng giác thuộc góc phần tư thứ II sao cho \(\widehat {AMO} = \frac{{3\pi }}{4}\).

\(sin\dfrac{129\pi}{4}=sin\dfrac{128\pi}{4}+sin\dfrac{\pi}{4}\\ =sin32\pi+sin\dfrac{\pi}{4}=sin\dfrac{\pi}{4}\)

\(\begin{array}{l}\cos \left( {{{225}^ \circ }} \right) = \cos \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = - \cos \left( {{{45}^ \circ }} \right) = - \frac{{\sqrt 2 }}{2}\\\sin \left( {{{225}^ \circ }} \right) = \sin \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = - \sin \left( {{{45}^ \circ }} \right) = - \frac{{\sqrt 2 }}{2}\\\tan \left( {225^\circ } \right) = \frac{{\sin \left( {{{225}^ \circ }} \right)}}{{\cos \left( {{{225}^ \circ }} \right)}} = 1\\\cot \left( {225^\circ } \right) = \frac{1}{{\tan \left( {225^\circ } \right)}} = 1\end{array}\)
\(\begin{array}{l}\cos \left( { - {{225}^ \circ }} \right) = \cos \left( {{{225}^ \circ }} \right) = \cos \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = - \cos \left( {{{45}^ \circ }} \right) = - \frac{{\sqrt 2 }}{2}\\\sin \left( { - {{225}^ \circ }} \right) = - \sin \left( {{{225}^ \circ }} \right) = - \sin \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = \sin \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { - 225^\circ } \right) = \frac{{\sin \left( {{{225}^ \circ }} \right)}}{{\cos \left( {{{225}^ \circ }} \right)}} = - 1\\\cot \left( { - 225^\circ } \right) = \frac{1}{{\tan \left( {225^\circ } \right)}} = - 1\end{array}\)
\(\begin{array}{l}\cos \left( { - {{1035}^ \circ }} \right) = \cos \left( {{{1035}^ \circ }} \right) = \cos \left( {{{6.360}^ \circ } - {{45}^ \circ }} \right) = \cos \left( { - {{45}^ \circ }} \right) = \cos \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\sin \left( { - {{1035}^ \circ }} \right) = - \sin \left( {{{1035}^ \circ }} \right) = - \sin \left( {{{6.360}^ \circ } - {{45}^ \circ }} \right) = - \sin \left( { - {{45}^ \circ }} \right) = \sin \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { - 1035^\circ } \right) = \frac{{\sin \left( { - {{1035}^ \circ }} \right)}}{{\cos \left( { - {{1035}^ \circ }} \right)}} = 1\\\cot \left( { - 1035^\circ } \right) = \frac{1}{{\tan \left( { - 1035^\circ } \right)}} = - 1\end{array}\)
\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{3}} \right) = \cos \left( {\pi + \frac{{2\pi }}{3}} \right) = - \cos \left( {\frac{{2\pi }}{3}} \right) = \frac{1}{2}\\\sin \left( {\frac{{5\pi }}{3}} \right) = \sin \left( {\pi + \frac{{2\pi }}{3}} \right) = - \sin \left( {\frac{{2\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2}\\\tan \left( {\frac{{5\pi }}{3}} \right) = \frac{{\sin \left( {\frac{{5\pi }}{3}} \right)}}{{\cos \left( {\frac{{5\pi }}{3}} \right)}} = - \sqrt 3 \\\cot \left( {\frac{{5\pi }}{3}} \right) = \frac{1}{{\tan \left( {\frac{{5\pi }}{3}} \right)}} = - \frac{{\sqrt 3 }}{3}\end{array}\)
\(\begin{array}{l}\cos \left( {\frac{{19\pi }}{2}} \right) = \cos \left( {8\pi + \frac{{3\pi }}{2}} \right) = \cos \left( {\frac{{3\pi }}{2}} \right) = \cos \left( {\pi + \frac{\pi }{2}} \right) = - \cos \left( {\frac{\pi }{2}} \right) = 0\\\sin \left( {\frac{{19\pi }}{2}} \right) = \sin \left( {8\pi + \frac{{3\pi }}{2}} \right) = \sin \left( {\frac{{3\pi }}{2}} \right) = \sin \left( {\pi + \frac{\pi }{2}} \right) = - \sin \left( {\frac{\pi }{2}} \right) = - 1\\\tan \left( {\frac{{19\pi }}{2}} \right)\\\cot \left( {\frac{{19\pi }}{2}} \right) = \frac{{\cos \left( {\frac{{19\pi }}{2}} \right)}}{{\sin \left( {\frac{{19\pi }}{2}} \right)}} = 0\end{array}\)
\(\begin{array}{l}\cos \left( { - \frac{{159\pi }}{4}} \right) = \cos \left( {\frac{{159\pi }}{4}} \right) = \cos \left( {40.\pi - \frac{\pi }{4}} \right) = \cos \left( { - \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\sin \left( { - \frac{{159\pi }}{4}} \right) = - \sin \left( {\frac{{159\pi }}{4}} \right) = - \sin \left( {40.\pi - \frac{\pi }{4}} \right) = - \sin \left( { - \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { - \frac{{159\pi }}{4}} \right) = \frac{{\cos \left( { - \frac{{159\pi }}{4}} \right)}}{{\sin \left( { - \frac{{159\pi }}{4}} \right)}} = 1\\\cot \left( { - \frac{{159\pi }}{4}} \right) = \frac{1}{{\tan \left( { - \frac{{159\pi }}{4}} \right)}} = 1\end{array}\)

Tham khảo:
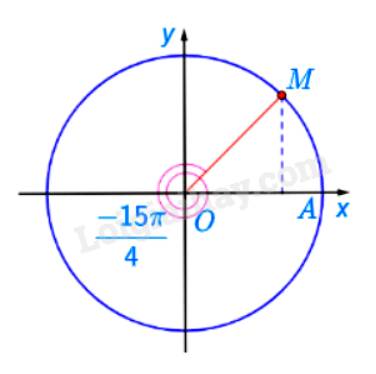
Điểm biểu diễn góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4} = - \frac{{7\pi }}{4} + ( - 1).2\pi \) được xác định là điểm M.
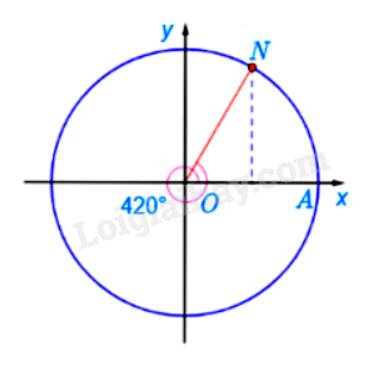
Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)

Tham khảo:
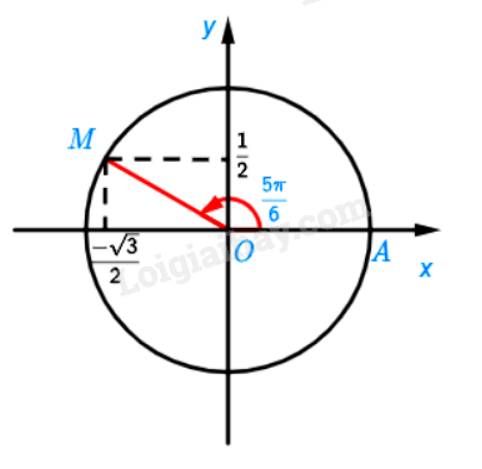
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)

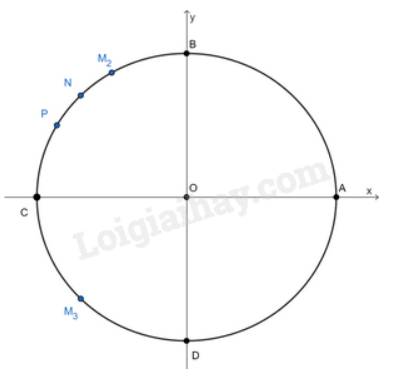
a) Ta có: \(\frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\). Ta chia đường tròn thành 3 phần bằng nhau. Khi đó điểm \({M_2}\) là điểm biểu diễn bởi góc có số đo \(\frac{{2\pi }}{3}\).
b) Ta có \( - \frac{{11\pi }}{4} = - \frac{{3\pi }}{4} + \left( { - 1} \right).2\pi \). Do đó điểm biểu diễn bởi góc \( - \frac{{11\pi }}{4}\) trùng với góc \( - \frac{{3\pi }}{4}\) và là điểm \({M_3}\).
c) Ta có \(\frac{{150}}{{180}} = \frac{5}{6}\). Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó P là điểm biểu diễn bởi góc \({150^0}\)
d) Ta có \( - {225^0} = - {180^0} - {45^0}\). Do đó điểm biểu diễn N là điểm biểu diễn bởi góc \( - {225^0}\)
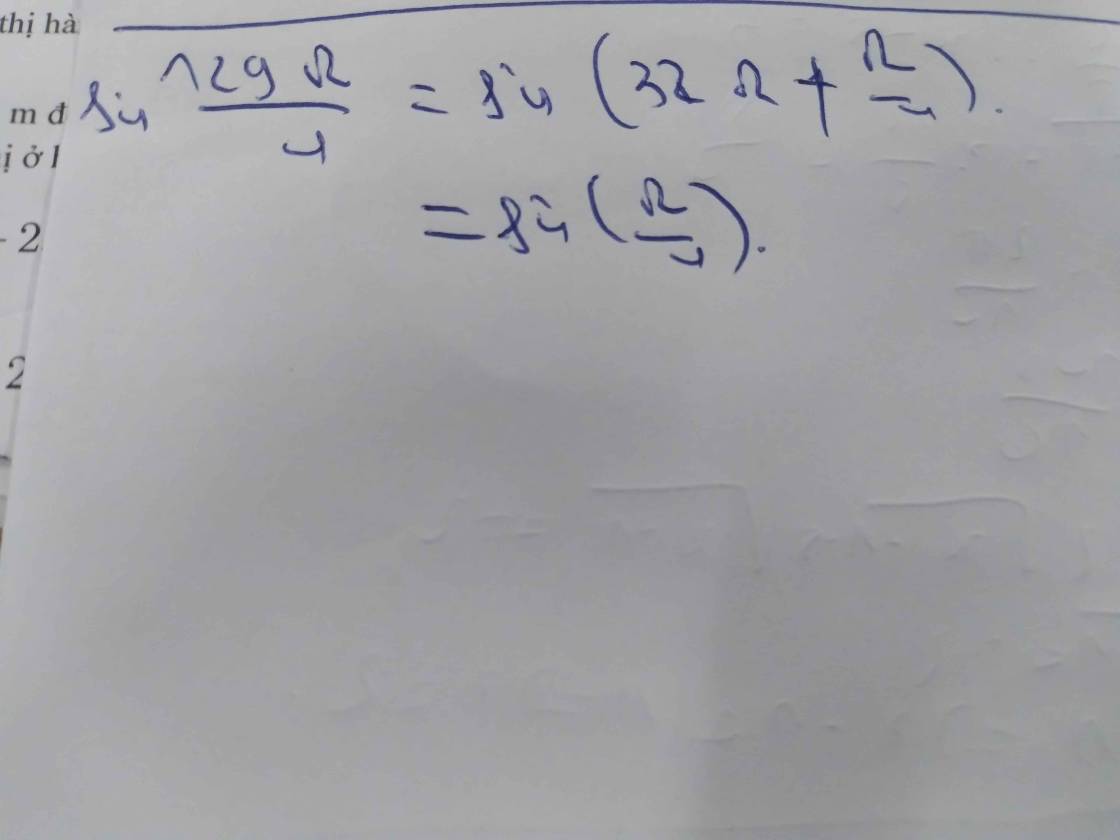

a) \(cos638^o=cos\left(-82^o\right)=cos\left(82^o\right)=sin8^o\)
b) \(cot\dfrac{19\pi}{5}=cot\dfrac{4\pi}{5}=-cot\dfrac{\pi}{5}\)