Cmr trong các tam giác vuông có cùng cạnh huyền, tam giác vuông cân có diện tích lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án là A.
Gọi x 0 < x < a là độ dài của một cạnh góc vuông.
Độ dài cạnh góc vuông còn lại là: a − x 2 − x 2 = a 2 − 2 a x .
Diện tích của tam giác là: S = 1 2 x a 2 − 2 a x .
Ta có S ' = 1 2 a 2 − 3 a x a 2 − 2 a x ; ⇒ S ' = 0 ⇔ x = a 3 .
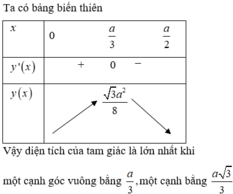
Bảng biến thiên:
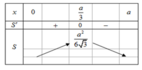
vậy S max = a 2 6 3

Đáp án A.
Giả sử cạnh góc vuông có độ dài bằng X x 0 < x < a .
Suy ra độ dài cạnh huyền là a - x .
Độ dài cạnh góc vuông còn lại là a - x 2 - x 2 = a 2 - 2 a x .
Diện tích tam giác vuông đó được tính bằng công thức S = 1 2 x . a 2 - 2 a x .
S = 1 2 a . a x . a x . a 2 - 2 a x ≤ 1 2 a . a x + a x + a 2 - 2 a x 3 3 = 1 2 a . a 6 27 = a 2 3 18 .
Dấu bằng xảy ra khi a x = a 2 - 2 a x ⇔ x = a 3 .

Đáp án D
Gọi độ dài một cạnh góc vuông của tam giác vuông là 
Khi đó độ dài cạnh huyền là a−x.
Độ dài cạnh góc vuông còn lại của tam giác vuông là ![]()
Ta có diện tích tam giác vuông ![]()

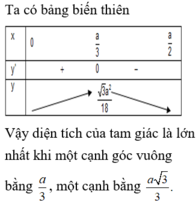
Ta có bảng biến thiên
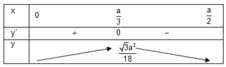
Vậy diện tích của tam giác là lớn nhất khi một cạnh góc vuông bằng
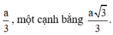

Độ dài cạnh huyền là:
\(\sqrt{2^2\cdot2}=2\sqrt{2}\simeq3\)