1) Cho tam giác ABC vuông tại A , đường trung trực BC cắt AC và BC tại D và E
a) C/m 2CE^2 = CA .CD
b) Cho AB = 24cm , BC= 40cm. Tính ED , DC , DA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 6 2022
Bài 1:
a: Xét ΔCED vuông tai E và ΔCAB vuông tại A có
góc C chung
Do đo: ΔCED\(\sim\)ΔCAB
Suy ra: CE/CA=CD/CB
hay \(CA\cdot CD=CE\cdot CB=2CE^2\)
b: EC=BC/2=20(cm)
Ta có: CE/CA=CD/CB
nên 20/32=CD/40
=>CD/40=5/8
=>CD=25(cm)
AD=AC-CD=32-25=7(cm)
9 tháng 7 2018
Xét tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 ( theo định lý py-ta-go)
BC2 = 242+ 322
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét tam giác vuông ACB và tam giác vuông ECD có:
Có \(\widehat{A}\) = \(\widehat{E}\) = 90o
\(\widehat{C}\) chung
=> Tam giác ACB = tam giác ECD (g.g)
=> AC/EC = AB/DE
=> DE = AB.EC/AC = 15cm
Vậy DE = 15cm
CM
1 tháng 8 2019
Xét hai tam giác vuông ABC và MDC, ta có:
∠ (BAC) = ∠ (DMC ) = 90 0
∠ C chung
Suy ra tam giác ABC đồng dạng với tam giác MDC (g.g)
Suy ra: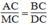 
Suy ra: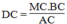 
Ta có: MC = 1/2 .BC = 1/2 .24 = 12 (cm)
Vây DC = (12.24)/9 = 32 (cm)
2 tháng 4 2021
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
Suy ra: \(\dfrac{AB}{HB}=\dfrac{BC}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BC\cdot BH\)(đpcm)
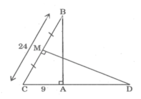
a: Xét ΔCED vuông tại E và ΔCAB vuong tại A có
góc C chung
Do đó;ΔCED dồngd ạng với ΔCAB
Suy ra: CE/CA=CD/CB
=>\(CE\cdot CB=CA\cdot CD=2\cdot CE^2\)
b: CE=BC/2=20cm
AC=32cm
Ta có: ΔCED đòng dạng với ΔCAB
nên CE/CA=CD/CB=ED/AB
=>CD/40=ED/24=20/32=5/8
=>CD=25cm; ED=15cm
=>DA=7cm