Bài 1: Cho a là góc nhọn . Rút gọn biểu thức
A= sin6a + cos6a+ 3sin2a-cos2 a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
1
28 tháng 8 2023
\(A=\left(sin^2a+cos^2a\right)^3-3\cdot sin^2a\cdot cos^2a\left(sin^2a+cos^2a\right)+3\cdot sin^2a\cdot cos^2a\)
\(=1-3\cdot sin^2a\cdot cos^2a+3\cdot sin^2a\cdot cos^2a\)
=1
LS
2
5 tháng 12 2021
b: \(=\left(\cos^2\alpha+\sin^2\alpha\right)^3-3\cos^2\alpha\sin^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)+3\cdot\sin^2\alpha\cdot\cos^2\alpha\)
=1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 12 2021
\(cos^4a-sin^4a+1=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)+1\)
\(=cos^2a-sin^2a+1=cos^2a-sin^2a+sin^2a+cos^2a\)
\(=2cos^2a\)
\(cos^6a+sin^6a+3sin^2a.cos^2a\)
\(=\left(cos^2a+sin^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)+3sin^2a.cos^2a\)
\(=1-3sin^2a.cos^2a.1+3sin^2a.cos^2a\)
\(=1\)
2 tháng 11 2021
\(a,A=\left(\cos^220^0+\cos^270^0\right)+\left(\cos^240^0+\cos^250^0\right)\\ A=\left(\cos^220^0+\sin^220^0\right)+\left(\cos^240^0+\sin^240^0\right)=1+1=2\\ b,B=\left(\cos^2\alpha\right)^3+\left(\sin^2\alpha\right)^3+3\sin^2\alpha\cdot\cos^2\alpha\cdot\left(\sin^2\alpha+\cos^2\alpha\right)\\ B=\left(\sin^2\alpha+\cos^2\alpha\right)^3=1^3=1\)
CM
28 tháng 5 2018
Chọn A.
Ta có: A= cos2( x-a) + cos2x -2cos a.cos x.cos( a - x).
= cos( x - a) [ cos(x - a) – 2cosa. cosx] + cos2x
= cos( x - a) [ cos x.cosa + sina.sinx – 2cosa.cosx] + cos2x
= cos( x - a) [ -cos x.cosa + sina.sinx] + cos2x
= -cos( x - a) .cos( x + a) + cos2x
CN
2
5 tháng 6 2020
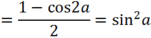
\(sin^2a+cos^2a-sin^4a-2cos^2a+sin^2a\)
\(=2sin^2a-cos^2a-sin^4a\)
\(=2sin^2a-cos^2a-\left(\frac{1-cos2a}{2}\right)^2\)
khai triển ra rồi quy đồng lên
\(=\frac{8sin^2a-4cos^2a-1+2cos2a-cos^22a}{4}\)
Mà \(2cos2a=2\left(cos^2a-1\right)=4cos^2-2\)
\(\Rightarrow\frac{8sin^2a-cos^22a-3}{4}\)
Mà \(-cos^22a=sin^22a-1=4sin^2cos^2-1\)
\(\Rightarrow\frac{8sin^2a+4sin^2a.cos^2a-4}{4}\)
\(=\frac{4sin^2a.\left(2-cos^2a\right)-4}{4}\)
\(=sin^2a\left(1+sin^2a\right)-1\)
\(=sin^4a-cos^2a\)
VT
2
11 tháng 9 2017
A= \(\left(\sin^2a\right)^3+\left(cos^2a\right)^3+3sin^2acos^2a\)
=\(\left(sin^2a+cos^2a\right)\left(sin^4a-cos^2asin^2a+cos^4a\right)+3sin^2acos^2a\)
\(sin^4a+2sin^2acos^2a+cos^4a=\left(sin^2+cos^2\right)^2=1^2=1\)
HH
0
ta có : \(A=sin^6a+cos^6a+3sin^2a-cos^2a\)
\(=\left(sin^2a\right)^3+\left(cos^3a\right)^2+3sin^2a-cos^2a\)
\(=\left(sin^2a+cos^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)+3sin^2a-cos^2a\)
\(=1-3sin^2a.cos^2a+3sin^2a-cos^2a\)
\(=3sin^2a-3sin^2a.cos^2a+1-cos^2a\)
\(=3sin^2a\left(1-cos^2a\right)+\left(1-cos^2a\right)\) \(=\left(3sin^2a+1\right)\left(1-cos^2a\right)\)
\(=\left(3sin^2a+1\right)\left(sin^2a\right)=3sin^4a+sin^2a\)