X phần Y = 8phần9 và x+y=-170
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LG
5 tháng 1 2017
y x 9 + y x 8 = 170
y x ( 9 + 8 ) = 170
y x 17 = 170
y = 170 : 17
y = 10
SG
5 tháng 1 2017
y x 9 + y x 8 = 170
y x ( 9 + 8 ) = 170
y x 17 = 170
y = 170 / 17
y = 10 
Smart gril
9 tháng 9 2023
\(xy+x+y=170\left(n\inℕ\right)\)
\(\Rightarrow x\left(y+1\right)+y+1-1=170\)
\(\Rightarrow\left(x+1\right)\left(y+1\right)=171\)
\(\Rightarrow\left(x+1\right);\left(y+1\right)\in U\left(171\right)=\left\{1;3;9;19;57;171\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(0;170\right);\left(2;56\right);\left(8;18\right);\left(18;8\right);\left(56;2\right);\left(170;0\right)\right\}\)
16 tháng 2 2021
a) Ta có: \(x:2=y:\left(-5\right)\)
nên \(\dfrac{x}{2}=\dfrac{y}{-5}\)
mà x-y=-7
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-1\\\dfrac{y}{-5}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)
Vậy: (x,y)=(-2;5)
b) Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}\)
nên \(\dfrac{x}{8}=\dfrac{y}{12}\)(1)
Ta có: \(\dfrac{y}{4}=\dfrac{z}{5}\)
nên \(\dfrac{y}{12}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
mà x+y-z=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{8}=2\\\dfrac{y}{12}=2\\\dfrac{z}{15}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)
Vậy: (x,y,z)=(16;24;30)
16 tháng 2 2021
b)
Do đó ta có 
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
NA
1
15 tháng 7 2016
1. Tìm giá trị lớn nhất :
Ta có : \(C^2=\left(\sqrt{x-4}+\sqrt{y-3}\right)^2=x-4+y-3+2\sqrt{\left(x-4\right)\left(y-3\right)}=8+2\sqrt{\left(x-4\right)\left(y-3\right)}\)
Theo bất đẳng thức Cauchy, ta có \(2\sqrt{\left(x-4\right)\left(y-3\right)}\le x-4+y-3=8\)
\(\Rightarrow C^2\le8+8=16\Rightarrow C\le4\) . Dấu "=" xảy ra khi và chỉ khi \(\begin{cases}x\ge4;y\ge3\\x+y=15\\x-4=y-3\end{cases}\) \(\Leftrightarrow\begin{cases}x=8\\y=7\end{cases}\)
Vậy C đạt giá trị lớn nhất bằng 4 khi và chỉ khi (x;y) = (8;7)
2. Tìm giá trị nhỏ nhất :
Ta có : \(C^2=8+2\sqrt{\left(x-4\right)\left(y-3\right)}\) . Vì \(2\sqrt{\left(x-4\right)\left(y-3\right)}\ge0\) nên \(C^2\ge8\Rightarrow C\ge2\sqrt{2}\)
Dấu "=" xảy ra khi và chỉ khi \(\begin{cases}x\ge4;y\ge3\\x+y=15\\\left(x-4\right)\left(y-3\right)=0\end{cases}\) \(\Leftrightarrow\begin{cases}x=4\\y=11\end{cases}\) hoặc \(\begin{cases}x=12\\y=3\end{cases}\)
Vậy C đạt giá trị nhỏ nhất bằng \(2\sqrt{2}\) khi và chỉ khi (x;y) = (4;11) hoặc (x;y) = (12;3)
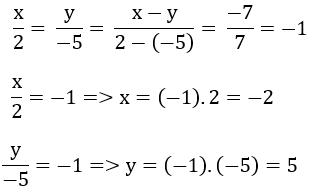
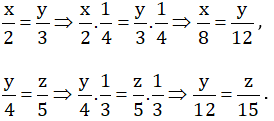
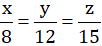
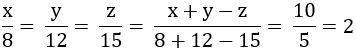
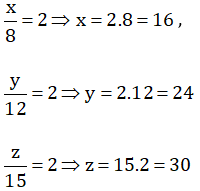
Theo đề bài: \(\dfrac{x}{y}=\dfrac{8}{9}\Rightarrow x=\dfrac{8y}{9}\) \(\left(1\right)\)và \(x+y=-170\)\(\left(2\right)\)
Thay \(\left(1\right)\) vào \(\left(2\right)\), ta có: \(\dfrac{8y}{9}+y=-170\)
\(\Leftrightarrow\dfrac{8y}{9}+\dfrac{9y}{9}=-170\)
\(\Leftrightarrow\dfrac{17y}{9}=-170\)
\(\Leftrightarrow17y=-1530\)
\(\Leftrightarrow y=-90\)
Thay \(y=-90\) vào \(\left(2\right)\) suy ra: \(x+\left(-90\right)=-170\)
\(\Rightarrow x=-80\)
Vậy \(x=-80;y=-90\)