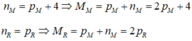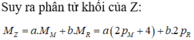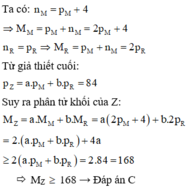1) Hợp chất Z dc tảo bởi 2 nguyên tố M và X có công thức là MaXb. Trong đó M chiếm 46,67% về khối lượng. Trong hạt nhân nguyên tử M có NM = PM + 4. Còn trong hạt nhân của X có Nx = Px. Biết rằng tổng số hạt proton trong phân tử Z bằng 58. Và a + b = 3 xác định công thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có các hệ phương trình
nM=pm+4 (1)
nX=px (2)
a.pM +b.pX=58 (3)
\(\%M=\dfrac{a\left(p_M+n_M\right)}{a\left(p_M+n_M\right)+b\left(p_X+n_X\right)}.100\%=46,67\%\)(4)
Thay (1)(2) vào (4), ta được :
\(\%M=\dfrac{a\left(2p_M+4\right)}{a\left(2p_M+4\right)+b.2p_X}.100\%=46,67\%\) (5)
Từ (3)(5) và a+b=3
TH1: \(\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}p_M=26\\p_X=16\end{matrix}\right.\)=> M là Fe, X là S => CTPT Z: FeS2
TH2: \(\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}p_M=12,5\\p_X=33\end{matrix}\right.\)=> Loại vì không thõa điều kiện p,n,e nguyên

Ta có : %M=46,67% => %X=53,33%
nM = pM + 4 ; nX= pX ; apM + bpX =58
Lại có : \(\frac{a\left(p_M+n_M\right)}{a\left(p_M+n_M\right)+b\left(p_X+n_X\right)}=46,67\%\) => \(\frac{a\left(p_M+n_M\right)}{2\left(ap_M+bp_X\right)+4}=46,67\%\)
=> a(pM+nM) = \(46,67\%\times[\left(2\times58\right)+4]\approx56\)
Tương tự ta có : b(pX+nX) = \(53,33\%\times[\left(2\times58\right)+4]\approx64\)
Theo bài ra ta có : a +b =3
=> +) Nếu a=2 => b=1 => M=56:2=28 ; X=64 (loại)
+) Nếu a=1 => b=2 => M 56 (Fe) ; X = 64:2=32 (S)
Vậy công thức phân tử Z là : FeS2

Gọi n, p là số notron và proton của M
n1, p1 là số notron và proton của R
Vì R chiếm 6,667% về khối lượng trong Z nên ta có :
\(\dfrac{b.\left(n_1+p_1\right)}{a\left(n+p\right)+b\left(n_1+p_1\right)}\)=6,667%
<=> 93,333b(n1+p1) - 6,667a(n+p) = 0 (1)
Tổng số proton trong phân tử Z là 84 :
=> ap + bp1 = 84(2)
Theo bài, ta có :
n = p + 4 (3)
n1 = p1 (4)
a + b =4 (5)
Từ (1)(3)(4) ta có PT: 186,666bp1 - 6,667a(2p+4) = 0 (6)
Vì a, b là các số nguyên dương và a + b =4
Nên ta có 3TH:
TH1: a=1 và b=3
TH2: a=b=2
TH3: a=3 và b=1
Thay a và b trong từng trường hợp trên vào PT (6) và PT(2) ta được hệ PT ẩn số p và p1( ĐK : p và p1 cũng là số nguyên dương)
=> Giải hệ chỉ có trường hợp (3) là thỏa mẵn với p= 26 và p1 = 6
p=26 => M = Fe
p1= 6 => R = C
Vậy công thức của Z là Fe3C

Chọn B
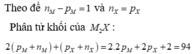
X chiếm 8/47 phần khối lượng => Nguyên tử khối X=16 và M=39
=> Số proton trong X là 8 (oxi), trong M là 19 (kali)
Hợp chất K 2 O có liên kết ion.

Đáp án B.
Theo đề nM - pM = 1 và nX = pX
Phân tử khối của M2X : 2(pM + nM) + (pX + nX) = 2.2pM + 2pX + 2 = 94
X chiếm 8/47 phần khối lượng => Nguyên tử khối X=16 và M=39
=> Số proton trong X là 8 (oxi), trong M là 19 (kali)
Hợp chất K2O có liên kết ion.

$\dfrac{M}{Xy} = \dfrac{46,67}{53,33} \Rightarrow \dfrac{n + p}{y(n' + p')} = \dfrac{46,67}{53,33} = \dfrac{7}{8}$
Thay $n - p = 4$ và $n' = p'$ vào, ta có :
$\dfrac{2p+ 4}{2xp'} = \dfrac{7}{8} \Rightarrow 4(2p + 4) = 7xp'$
Tổng số proton trong MAx là 58 nên: p + xp’ = 58. Từ đây tìm được: p = 26 và xp’ = 32.
Do A là phi kim ở chu kì 3 nên 15 ≤ p’ ≤ 17. Vậy x = 2 và p’ = 16 thỏa mãn.
Vậy M là Fe và A là S; công thức của MAx là FeS2.
hnamyuh CTV, bn ơi cho mk hỏi là tại sao ta lại có tỉ số: \(\dfrac{M}{X_y}=\dfrac{46,67}{53,33}\) ??? Cám ơn bn trước!!!

M chiếm 46,67% về khối lượng:

Quan sát – phân tích: Hệ 5 ẩn gồm 4 phương trình không thể giải thông thường để tìm nghiện vì ta cần phải rút gọn nghiệm: Phương trình (2) chứa ẩn ZM và x. ZA từ phương trình (1); (3); (4) ta có thể đưa về 1 phương trình chứa 2 ẩn ZM và x
Z A → Đưa về hệ phương trình 2 ẩn.
Ta đưa được về hệ sau
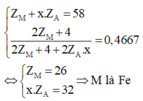
M là Fe nên x sẽ nhận giá trị từ 1 đến 3.
Từ x.ZA = 32 ta có các giá trị của ZA

Vậy H là FeS2
Đáp án A.