Cho hàm số y = \(\dfrac{1}{6}\) x4 - \(\dfrac{7}{3}\) x2 có đồ thị (C) . Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại 2 điểm phân biệt M(x1 ; y1) , N(x2 ; y2) ( M , N khác A ) thỏa mãn y1 - y2 = 4(x1 - x2)
A . 3
B . 0
C . 1
D . 2
( giải chi tiếp giúp mình nhé , cảm ơn ạ )

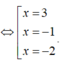
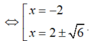


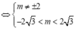

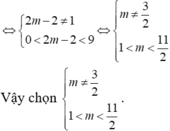
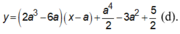
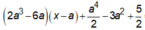
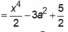
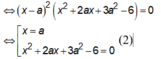
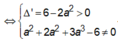
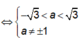


Chọn B